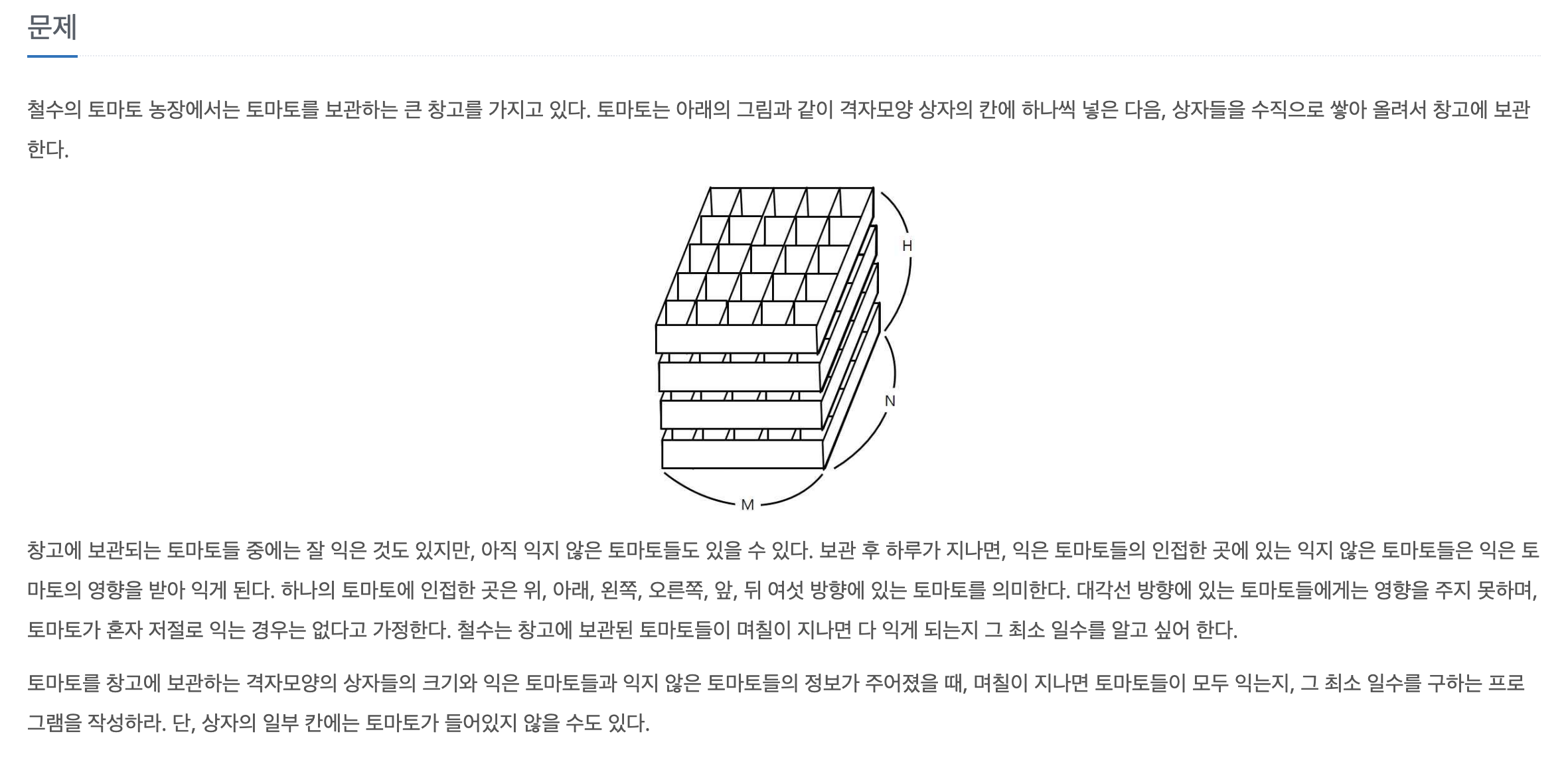
토마토 문제는 대표적인 bfs 거리 구하기 문제의 응용인데
저번 문제로 2차원에서 토마토를 다루었지만 이번에는 3차원에서 토마토로 다루도록 해보겠습니다.
해당 문제를 푸는 데에 핵심적인 개념은 bfs에서 dict라는 array를 통해 거리를 구하는 것에서
단순히 일 수로 바꾸면 되는건데 시작점이 한 개가 아니라 여러개라는 점입니다.
시작점이 여러개라는걸 해결하는 방법도 간단합니다. 시작점들을 미리 큐에 두고 bfs를 돌리면 됩니다.
어차피 최소 일수를 구하는 것이기 때문에 어떠한 시작점에서 방문했다면 다른 시작점에서 방문하지 않을 것이고
큐에서 bfs를 진행하는 과정은 일 수에 따라서 큐에 들어갑니다.
풀이
#include <bits/stdc++.h>
using namespace std;
int box[101][101][101]; //입력 받는 박스
int dist[101][101][101]; //익은 토마토로부터의 거리를 기록할 3차원 배열 0으로 초기화되어있다.
queue<tuple<int, int, int>> q; // bfs를 위한 queue
int dx[6] = {1, -1, 0, 0, 0, 0};
int dy[6] = {0, 0, -1, 1, 0, 0};
int dz[6] = {0, 0, 0, 0, -1, 1}; //dx dy dz로 3차원 상하좌우를 표시함
int day; //ans임. 큐에서 마지막으로 들어가는 일 수
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
int m, n, h;
cin >> m >> n >> h; // 입력
for (int i=0; i<h; i++)
{
for(int j=0; j<n; j++)
{
for(int k=0; k<m; k++)
{
cin >> box[i][j][k]; // 입력
if (box[i][j][k] == 1)
q.push({i, j, k}); // 익은 토마토를 큐에 push 해둠
else if (box[i][j][k] == 0) // 안 익은 토마토는
dist[i][j][k] = -1; // 방문하지 않았으므로 -1로 체크
}
}
}
while (!q.empty())
{
auto cur = q.front(); q.pop(); // 큐에서 빼냄
int curx, cury, curz; // 현재 좌표
tie(curx, cury, curz) = cur;
for(int i=0; i<6; i++)
{
int nx = curx + dx[i];
int ny = cury + dy[i];
int nz = curz + dz[i]; //새로운 좌표
//새로운 좌표가
if (nx < 0 || nx >= h || ny < 0 || ny >= n || nz < 0 || nz >= m) // 배열 범위 초과
continue;
if (dist[nx][ny][nz] >= 0) //이미 방문함
continue;
q.push({nx, ny, nz}); // 큐에 넣고
dist[nx][ny][nz] = dist[curx][cury][curz] + 1; // 방문하였음을 표시
day = dist[nx][ny][nz];
}
}
for (int i=0; i<h; i++)
{
for (int j=0; j<n; j++)
{
for (int k=0; k<m; k++)
{
if (dist[i][j][k] == -1) // 방문되지 않은 토마토가 있으면
{
cout << -1; // -1을 출력하고 종료
return 0;
}
}
}
}
cout << day; // 정답 출력
return 0;
}풀이는 위와 같고
주석으로 코드 설명을 달아 두었습니다.
tie함수와 tuple는 처음 써보는데 2개일 때는 pair을 써도 되지만 3개부터는 tuple을 사용해야합니다.
tie함수는 tuple에서 변수들에 값을 묶어서 넣을 때(?) 사용합니다.

토마토 문제는 대표적인 bfs 거리 구하기 문제의 응용인데
저번 문제로 2차원에서 토마토를 다루었지만 이번에는 3차원에서 토마토로 다루도록 해보겠습니다.
해당 문제를 푸는 데에 핵심적인 개념은 bfs에서 dict라는 array를 통해 거리를 구하는 것에서
단순히 일 수로 바꾸면 되는건데 시작점이 한 개가 아니라 여러개라는 점입니다.
시작점이 여러개라는걸 해결하는 방법도 간단합니다. 시작점들을 미리 큐에 두고 bfs를 돌리면 됩니다.
어차피 최소 일수를 구하는 것이기 때문에 어떠한 시작점에서 방문했다면 다른 시작점에서 방문하지 않을 것이고
큐에서 bfs를 진행하는 과정은 일 수에 따라서 큐에 들어갑니다.
풀이
#include <bits/stdc++.h>
using namespace std;
int box[101][101][101]; //입력 받는 박스
int dist[101][101][101]; //익은 토마토로부터의 거리를 기록할 3차원 배열 0으로 초기화되어있다.
queue<tuple<int, int, int>> q; // bfs를 위한 queue
int dx[6] = {1, -1, 0, 0, 0, 0};
int dy[6] = {0, 0, -1, 1, 0, 0};
int dz[6] = {0, 0, 0, 0, -1, 1}; //dx dy dz로 3차원 상하좌우를 표시함
int day; //ans임. 큐에서 마지막으로 들어가는 일 수
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
int m, n, h;
cin >> m >> n >> h; // 입력
for (int i=0; i<h; i++)
{
for(int j=0; j<n; j++)
{
for(int k=0; k<m; k++)
{
cin >> box[i][j][k]; // 입력
if (box[i][j][k] == 1)
q.push({i, j, k}); // 익은 토마토를 큐에 push 해둠
else if (box[i][j][k] == 0) // 안 익은 토마토는
dist[i][j][k] = -1; // 방문하지 않았으므로 -1로 체크
}
}
}
while (!q.empty())
{
auto cur = q.front(); q.pop(); // 큐에서 빼냄
int curx, cury, curz; // 현재 좌표
tie(curx, cury, curz) = cur;
for(int i=0; i<6; i++)
{
int nx = curx + dx[i];
int ny = cury + dy[i];
int nz = curz + dz[i]; //새로운 좌표
//새로운 좌표가
if (nx < 0 || nx >= h || ny < 0 || ny >= n || nz < 0 || nz >= m) // 배열 범위 초과
continue;
if (dist[nx][ny][nz] >= 0) //이미 방문함
continue;
q.push({nx, ny, nz}); // 큐에 넣고
dist[nx][ny][nz] = dist[curx][cury][curz] + 1; // 방문하였음을 표시
day = dist[nx][ny][nz];
}
}
for (int i=0; i<h; i++)
{
for (int j=0; j<n; j++)
{
for (int k=0; k<m; k++)
{
if (dist[i][j][k] == -1) // 방문되지 않은 토마토가 있으면
{
cout << -1; // -1을 출력하고 종료
return 0;
}
}
}
}
cout << day; // 정답 출력
return 0;
}풀이는 위와 같고
주석으로 코드 설명을 달아 두었습니다.
tie함수와 tuple는 처음 써보는데 2개일 때는 pair을 써도 되지만 3개부터는 tuple을 사용해야합니다.
tie함수는 tuple에서 변수들에 값을 묶어서 넣을 때(?) 사용합니다.
