문제 설명
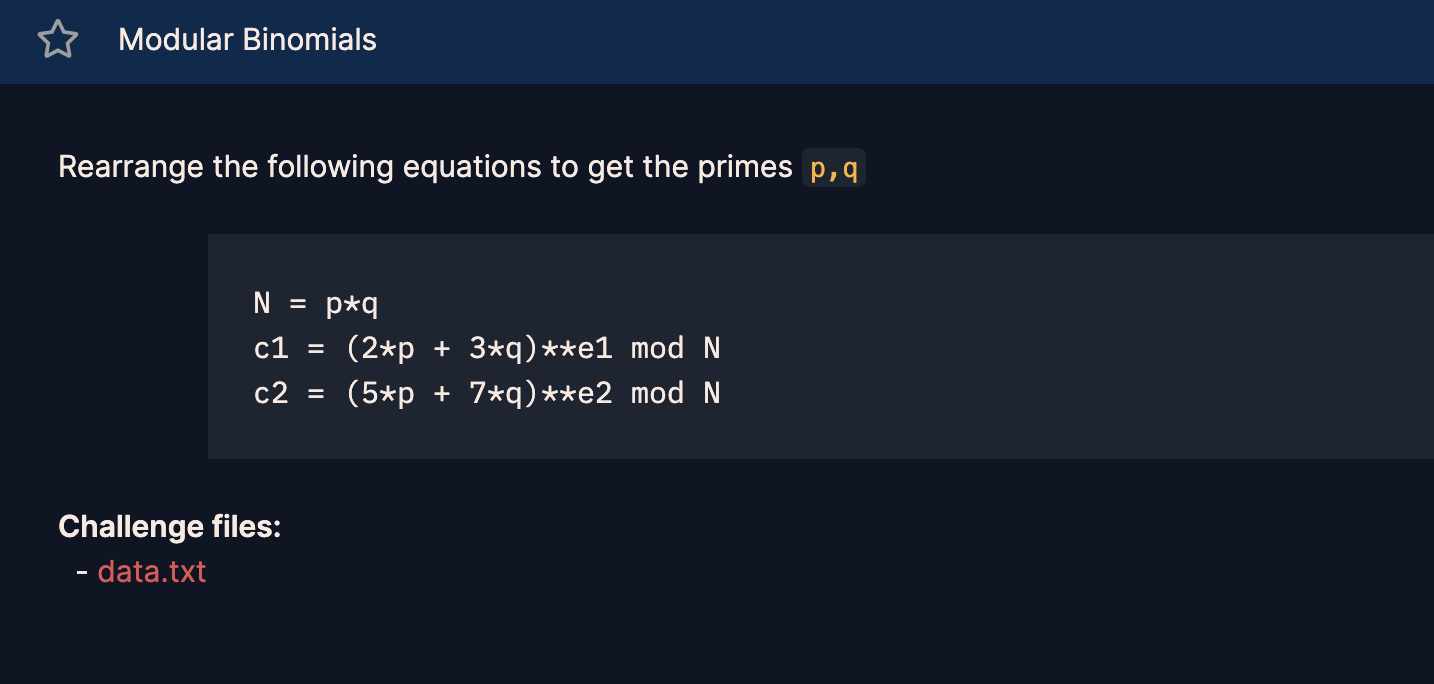
다음 방정식을 재배열하여 소수 p, q를 구하여라.
N = p*q
c1 = (2*p + 3*q)**e1 mod N
c2 = (5*p + 7*q)**e2 mod N
문제 풀이
이번 문제를 풀기 위해서 정말 많은 개념들을 찾아봤다.
나는 합동식에 익숙치가 않아서 너무 어려웠던 문제이다..
$N = pq$이고, $c_1 = (2p + 3q)^{e_1} \bmod N$, $c_2 = (5p + 7q)^{e_2} \bmod N$이다.
우리는 p나 q를 중 하나를 구하면 N을 나눠서 다른 하나를 구할 수 있다.
연립 방정식을 푸는 것처럼 풀이가 가능하다. 위에 식은 이항으로 n제곱 되어있는데 이게 어떻게 연립방정식처럼 풀 수 있는가?
Freshman's dream(대학교 1학년의 꿈)이 성립한다.
$(x+y)^n = x^n + y^n$이라는 허무맹랑한 식을 대학교 1학년의 꿈이라고 한다.
여기서는 modular 연산에 의해 성립한다.
$c_1 = (2p + 3q)^{e_1} \bmod N$에서
중간 항이 날아가는 것을 보여야 하는데,
매우 직관적이다. $N = pq$이고. 이항정리에 의해 첫 항이 $(2p)^{e_1}$이고 끝 항은 $(3q)^{e_1}$일 것이다. 그리고 중간 항은 $p$와 $q$을 곱한 값.. $\sum_{r=1}^{e_1-1} {e_1 \choose r}(2p)^{r}(3q)^{e_1-r}$인데 이건 $\bmod N$에 대하여 0이다.
$\therefore c_1 = (2p)^{e_1}+(3q)^{e_1} \bmod N$
$c_2 = (5p)^{e_2} + (7q)^{e_2} \bmod N$ 가 성립한다.
p, q를 구하기 위해, 하나의 식에 대해서만 정리하도록 하자. 우리가 연립방정식을 푸는 것처럼 소거되도록 한다.
$c_1$식에서는 양변에 $e_2$를 제곱하고 $c_2$식에서는 $e_1$제곱한다.
$c_1^{e_2} \equiv (2p)^{e_1e_2} + (3q)^{e_1e_2} \bmod N$
$c_2^{e_1} \equiv (5p)^{e_1e_2} + (7q)^{e_1e_2} \bmod N$
p를 소거하기 위해 $c_1$식에는 $5^{e_1e_2}$를 곱하고 $c_2$식에는 $2^{e_1e_2}$를 곱한다.
그리고 소거하면
$5^{e_1e_2}c_1^{e_2} -2^{e_1e_2}c_2^{e_1} \equiv (15q)^{e_1e_2} - (14q)^{e_1e_2} \bmod N$
$\therefore (15^{e_1e_2}-14^{e_1e_2})q^{e_1e_2} \equiv 5^{e_1e_2}c_1^{e_2} -2^{e_1e_2}c_2^{e_1} \bmod N$
$5^{e_1e_2}c_1^{e_2} -2^{e_1e_2}c_2^{e_1}$은 $\bmod N$에 대하여 $q$에 대한 곱셈의 형태로 나타내어진다.
우리는 N을 pq라고 정의하였으므로 mod N에 대한 q와 N의 최대공약수(gcd)는 q일 것이다.
$\gcd(5^{e_1e_2}c_1^{e_2} -2^{e_1e_2}c_2^{e_1}, N) = q$
$p = N // q$
이렇게 구할 수 있다.
import math
n = 14905562257842714057932724129575002825405393502650869767115942606408600343380327866258982402447992564988466588305174271674657844352454543958847568190372446723549627752274442789184236490768272313187410077124234699854724907039770193680822495470532218905083459730998003622926152590597710213127952141056029516116785229504645179830037937222022291571738973603920664929150436463632305664687903244972880062028301085749434688159905768052041207513149370212313943117665914802379158613359049957688563885391972151218676545972118494969247440489763431359679770422939441710783575668679693678435669541781490217731619224470152467768073
e1 = 12886657667389660800780796462970504910193928992888518978200029826975978624718627799215564700096007849924866627154987365059524315097631111242449314835868137
e2 = 12110586673991788415780355139635579057920926864887110308343229256046868242179445444897790171351302575188607117081580121488253540215781625598048021161675697
c1 = 14010729418703228234352465883041270611113735889838753433295478495763409056136734155612156934673988344882629541204985909650433819205298939877837314145082403528055884752079219150739849992921393509593620449489882380176216648401057401569934043087087362272303101549800941212057354903559653373299153430753882035233354304783275982332995766778499425529570008008029401325668301144188970480975565215953953985078281395545902102245755862663621187438677596628109967066418993851632543137353041712721919291521767262678140115188735994447949166616101182806820741928292882642234238450207472914232596747755261325098225968268926580993051
c2 = 14386997138637978860748278986945098648507142864584111124202580365103793165811666987664851210230009375267398957979494066880296418013345006977654742303441030008490816239306394492168516278328851513359596253775965916326353050138738183351643338294802012193721879700283088378587949921991198231956871429805847767716137817313612304833733918657887480468724409753522369325138502059408241232155633806496752350562284794715321835226991147547651155287812485862794935695241612676255374480132722940682140395725089329445356434489384831036205387293760789976615210310436732813848937666608611803196199865435145094486231635966885932646519
d = pow(5, e1 * e2, n) * pow(c1, e2, n) - pow(2, e1 * e2, n) * pow(c2, e1, n)
q = math.gcd(d, n)
p = n // q
print("crypto{%d,%d}" % (p,q))python으로 나타내면 위와 같다.
그토록 어려웠던 Modular Arithmetic을 마쳤다..

문제 설명
다음 방정식을 재배열하여 소수 p, q를 구하여라.
N = p*q
c1 = (2*p + 3*q)**e1 mod N
c2 = (5*p + 7*q)**e2 mod N
문제 풀이
이번 문제를 풀기 위해서 정말 많은 개념들을 찾아봤다.
나는 합동식에 익숙치가 않아서 너무 어려웠던 문제이다..
$N = pq$이고, $c_1 = (2p + 3q)^{e_1} \bmod N$, $c_2 = (5p + 7q)^{e_2} \bmod N$이다.
우리는 p나 q를 중 하나를 구하면 N을 나눠서 다른 하나를 구할 수 있다.
연립 방정식을 푸는 것처럼 풀이가 가능하다. 위에 식은 이항으로 n제곱 되어있는데 이게 어떻게 연립방정식처럼 풀 수 있는가?
Freshman's dream(대학교 1학년의 꿈)이 성립한다.
$(x+y)^n = x^n + y^n$이라는 허무맹랑한 식을 대학교 1학년의 꿈이라고 한다.
여기서는 modular 연산에 의해 성립한다.
$c_1 = (2p + 3q)^{e_1} \bmod N$에서
중간 항이 날아가는 것을 보여야 하는데,
매우 직관적이다. $N = pq$이고. 이항정리에 의해 첫 항이 $(2p)^{e_1}$이고 끝 항은 $(3q)^{e_1}$일 것이다. 그리고 중간 항은 $p$와 $q$을 곱한 값.. $\sum_{r=1}^{e_1-1} {e_1 \choose r}(2p)^{r}(3q)^{e_1-r}$인데 이건 $\bmod N$에 대하여 0이다.
$\therefore c_1 = (2p)^{e_1}+(3q)^{e_1} \bmod N$
$c_2 = (5p)^{e_2} + (7q)^{e_2} \bmod N$ 가 성립한다.
p, q를 구하기 위해, 하나의 식에 대해서만 정리하도록 하자. 우리가 연립방정식을 푸는 것처럼 소거되도록 한다.
$c_1$식에서는 양변에 $e_2$를 제곱하고 $c_2$식에서는 $e_1$제곱한다.
$c_1^{e_2} \equiv (2p)^{e_1e_2} + (3q)^{e_1e_2} \bmod N$
$c_2^{e_1} \equiv (5p)^{e_1e_2} + (7q)^{e_1e_2} \bmod N$
p를 소거하기 위해 $c_1$식에는 $5^{e_1e_2}$를 곱하고 $c_2$식에는 $2^{e_1e_2}$를 곱한다.
그리고 소거하면
$5^{e_1e_2}c_1^{e_2} -2^{e_1e_2}c_2^{e_1} \equiv (15q)^{e_1e_2} - (14q)^{e_1e_2} \bmod N$
$\therefore (15^{e_1e_2}-14^{e_1e_2})q^{e_1e_2} \equiv 5^{e_1e_2}c_1^{e_2} -2^{e_1e_2}c_2^{e_1} \bmod N$
$5^{e_1e_2}c_1^{e_2} -2^{e_1e_2}c_2^{e_1}$은 $\bmod N$에 대하여 $q$에 대한 곱셈의 형태로 나타내어진다.
우리는 N을 pq라고 정의하였으므로 mod N에 대한 q와 N의 최대공약수(gcd)는 q일 것이다.
$\gcd(5^{e_1e_2}c_1^{e_2} -2^{e_1e_2}c_2^{e_1}, N) = q$
$p = N // q$
이렇게 구할 수 있다.
import math
n = 14905562257842714057932724129575002825405393502650869767115942606408600343380327866258982402447992564988466588305174271674657844352454543958847568190372446723549627752274442789184236490768272313187410077124234699854724907039770193680822495470532218905083459730998003622926152590597710213127952141056029516116785229504645179830037937222022291571738973603920664929150436463632305664687903244972880062028301085749434688159905768052041207513149370212313943117665914802379158613359049957688563885391972151218676545972118494969247440489763431359679770422939441710783575668679693678435669541781490217731619224470152467768073
e1 = 12886657667389660800780796462970504910193928992888518978200029826975978624718627799215564700096007849924866627154987365059524315097631111242449314835868137
e2 = 12110586673991788415780355139635579057920926864887110308343229256046868242179445444897790171351302575188607117081580121488253540215781625598048021161675697
c1 = 14010729418703228234352465883041270611113735889838753433295478495763409056136734155612156934673988344882629541204985909650433819205298939877837314145082403528055884752079219150739849992921393509593620449489882380176216648401057401569934043087087362272303101549800941212057354903559653373299153430753882035233354304783275982332995766778499425529570008008029401325668301144188970480975565215953953985078281395545902102245755862663621187438677596628109967066418993851632543137353041712721919291521767262678140115188735994447949166616101182806820741928292882642234238450207472914232596747755261325098225968268926580993051
c2 = 14386997138637978860748278986945098648507142864584111124202580365103793165811666987664851210230009375267398957979494066880296418013345006977654742303441030008490816239306394492168516278328851513359596253775965916326353050138738183351643338294802012193721879700283088378587949921991198231956871429805847767716137817313612304833733918657887480468724409753522369325138502059408241232155633806496752350562284794715321835226991147547651155287812485862794935695241612676255374480132722940682140395725089329445356434489384831036205387293760789976615210310436732813848937666608611803196199865435145094486231635966885932646519
d = pow(5, e1 * e2, n) * pow(c1, e2, n) - pow(2, e1 * e2, n) * pow(c2, e1, n)
q = math.gcd(d, n)
p = n // q
print("crypto{%d,%d}" % (p,q))python으로 나타내면 위와 같다.

그토록 어려웠던 Modular Arithmetic을 마쳤다..
