설명
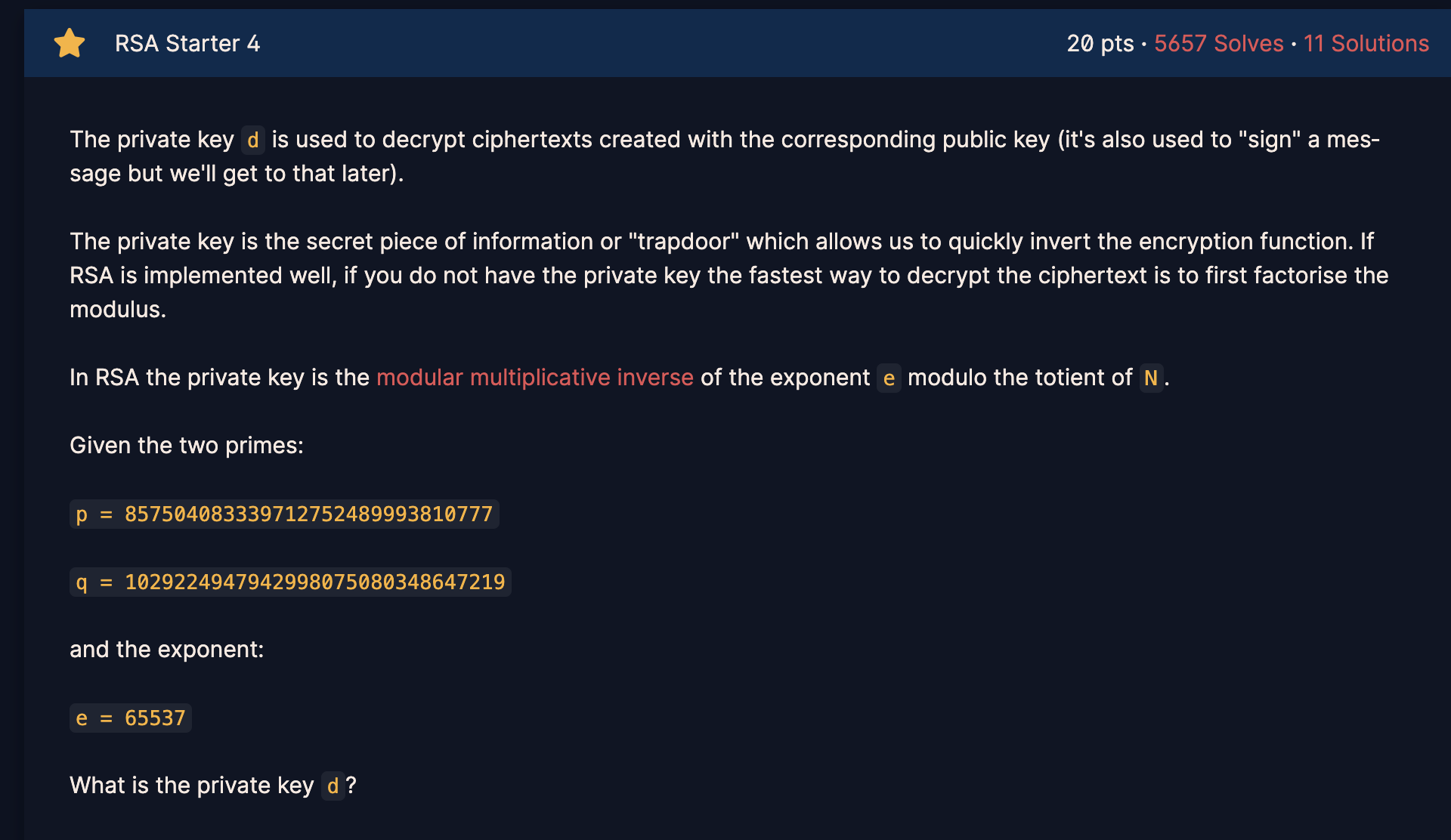
개인 키 d는 해당 공개 키로 생성된 암호문을 해독하는데 사용된다. (메시지를 "서명"하는데도 사용되지만 이는 나중에 설명할 것이다.)
개인 키는 암호화 기능을 빠르게 반전시킬 수 있는 "트랩도어"이다. RSA 가 잘 구현되어 있고 개인 키가 없을 때, 암호문을 해독하는 갖아 빠른 방법은 모듈러를 분해하는 것이다.
두 개의 소수가 주어진다. :
p = 857504083339712752489993810777
q = 1029224947942998075080348647219
그리고 지수:
e = 65537
개인 키 d는 무엇인가?
풀이
RSA에서 $d$는 $\phi(N)$에 대한 $e$의 역원이다.
$\therefore d = e^{-1} \bmod \phi(N)$ 이에 대해서는 RSA 원리를 찾아보면 많이 나온다
이전에 페르마의 소정리(FLT)를 공부할 때 오일러 정리에 대해서도 본 적이 있다.
오일러 정리는 다음과 같다.
정수 $a$ 및 양의 정수 $N$이 주어져있고 $a, N$이 서로소이면,
$a^{\phi(N)} \equiv 1 \pmod N$ 이 성립한다.
공개키로 암호화된 상태는 평문 $m$에 대한 암호문 $c$는 $c = m^e \bmod N$이다. 이를 복호화하기 위해 d제곱한다.
$m^{de}$ $d = e^{-1}$이므로 $de \equiv 1 \bmod \phi N$이다.
오일러 정리에 의해 $m^{ de} = m^{\phi(N) + 1} = m^{\phi(N)} * m^1 \equiv m \bmod N$ 이 성립한다.
뭐 암튼..
d 를 구해보자.
p = 857504083339712752489993810777
q = 1029224947942998075080348647219
e = 65537
phi = (p-1) * (q-1)
def extended_gcd(a, b):
if a == 0:
return b, 0, 1
else:
gcd, x, y = extended_gcd(b % a, a)
return gcd, y - (b // a) * x, x
print(extended_gcd(e, phi)[1])
# print(pow(e, -1, phi))
역원을 구하기 위해 extended GCD를 써도 되고. pow 함수를 써도 된다.
p = 857504083339712752489993810777
q = 1029224947942998075080348647219
e = 65537
phi = (p-1) * (q-1)
print(xgcd(e, phi)[1])최근 sage 사용법도 익히는 겸 sage로도 풀어보았다.
sage에서 extended gcd 를 사용하려면 xgcd를 사용한다.
