
제가 2019년 캠퍼스형 공동 교육과정에서 자료구조를 이수하며 정리한 것입니다.
최소 신장 트리 알고리즘
다정고등학교 이정민
- 크러스컬 알고리즘(Kruskal’s algorithm)
크러스컬 알고리즘은 변의 개수를 E 꼭짓점의 개수를 V라고 할 때 O(E log V) 의 시간 복잡도를 가진다.
크러스컬 알고리즘은 아래와 같이 작동한다.
1. 그래프의 각 꼭짓점이 각각 하나의 나무가 되도록 하는 숲A 를 만든다.
2. 모든 변을 원소로 하는 집합 S를 만든다.
3. 집합 S 가 비어있지 않는 동안
- 가장 작은 비용의 변을 S에서 하나 뺀다.
- 그 변이 어떤 두개의 나무를 연결한다면 두 나무를 연결하여 하나의 나무로 만든다.
- 그렇지 않다면 그 변은 버린다.
이와 다른 형태로, 변을 제거하는 방식이 존재한다.
1. 그래프에서 꼭짓점 또는 나무를 분리해 내지 않는 최대 가중치의 변을 제거한다.
2. 그래프에 n-1개 변만 남을 때까지 과정 1을 반복한다.
3. 그래프에 n-1개의 변이 남으면 최소 신장 트리이다.
예를 들어, 다음과 같은 그래프가 있다.
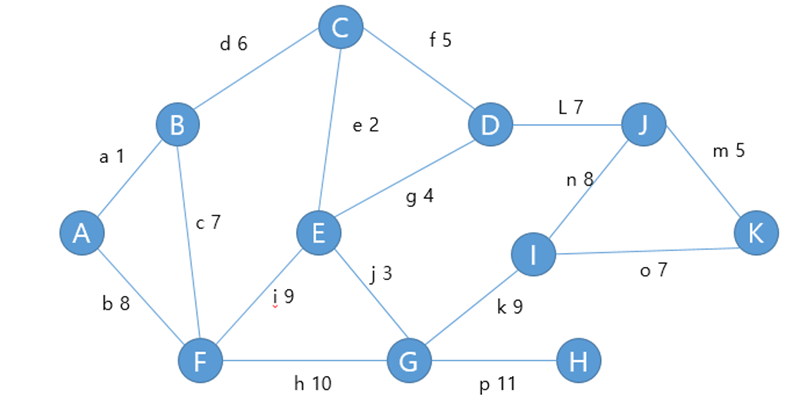
먼저 가장 비용이 낮은 a를 선택한다. 현재까지 비용은 1이다. 다음으로 계속해서 비용이 낮은 간선을 선택하되 고리가 만들어지지 않도록 한다.
이 점에 유의하여 선택하는 간선의 순서는 a – e – j – g – m (f는 순환이 만들어진다.) - d – c, l, o – p (n, b, k,i,h 는 순환이 만들어진다.) 순서이다.
따라서 비용은 1+2+3+4+5+6+7+7+7+11 = 53 이다.
- 프림 알고리즘 (Prim’s algorithm)
프림 알고리즘은 변의 개수를 E, 꼭짓점의 개수를 V 라고 하였을 때, 이진 힙을 사용하면 O(E log V)의 시간 복잡도를 가진다. 또한 그래프가 충분히 빽빽한 경우, 피보나치 힙을 사용하여 더 빠르게 할 수 있다, 이 방법은 복잡도가 O(E + V log V) 까지 떨어진다.
프림 알고리즘은 아래와 같은 순서로 작동한다.
1. 그래프에서 하나의 꼭짓점을 선택하여 트리를 만든다.
2. 그래프의 모든 변이 들어 있는 집합을 만든다.
3. 모든 꼭짓점이 트리에 포함되어 있지 않은 동안
- 트리와 연결된 변 가운데 트리 속의 두 꼭짓점을 연결하지 않는 가장 가중치가 작은 변을 트리에 추가한다.
알고리즘이 종료되었을 때, 만들어진 트리가 최소 신장 트리가 된다.
다음과 같은 그래프에서
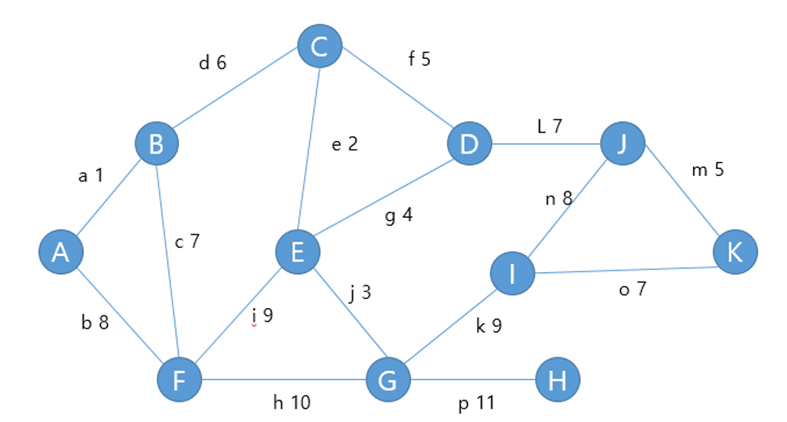
임의의 노드를 잡는다. A를 잡겠다.
노드를 A로 잡을 경우 잡은 노드를 집합 T에 포함시킨다. 즉, T에는 노드 A가 들어있다. 이후 T에 있는 노드와 T에 없는 노드 사이에 간선 중 최소 비용인 간선을 찾는다. 찾은 간선이 연결하는 노드 중 T에 없는 노드를 T에 포함시키고 최소비용인 간선을 찾는 과정을 반복하면 된다.
A를 노드로 잡을 경우, 최소비용인 간선 a가 선택된다. 따라서 노드 B가 T에 포함되게 된다. 같은 원리로 찾다보면 다음과 같은 노드의 순서를 가진다.
A – B – C – E – G – D – F – J – K – I – H 따라서 최소비용은
1 + 6 + 2 + 3 +4 + 7 + 7+ 5 + 7+ 11 = 53이다.
- 솔린 알고리즘(Sollin’s algorithm)
솔린 알고리즘의 시간 복잡도는 변의 개수를 E 꼭짓점의 개수를 V라고 할 때 O(E log V)의 시간 복잡도를 가진다. 각 스텝마다 가능한 최선의 선택지를 고르는 것을 반복하여 결과를 얻어낸다.
솔린 알고리즘은 다음과 같이 작동한다.
1. 시작하면서 모든 정점을 트리로 정의한다. (포레스트 상태)
2. 하나의 트리에 대해 외부의 꼭짓점과 연결 가능한 가장 비용이 작은 간선을 선택해 추가한다.
- 간선이 중복되는 경우에는 하나만 선택한다.
3. 트리가 하나로 이어질 때까지 2를 반복한다.
알고리즘이 종료되었을 때, 최소 신장 트리가 된다.
다음과 같은 그래프에서
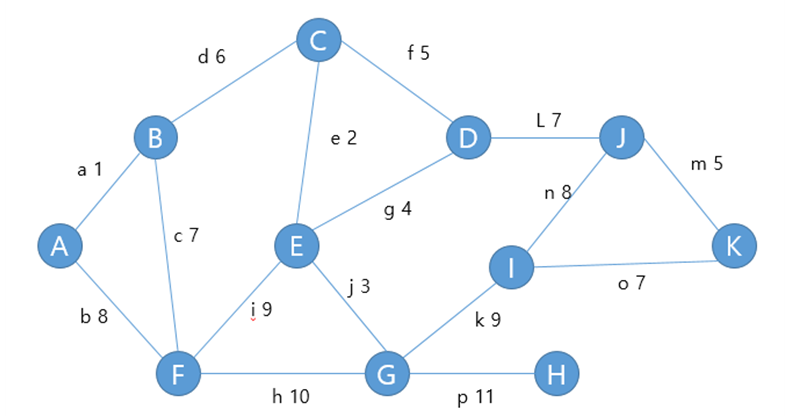
노드 A에 대해 비용이 가장 작은 간선 a가 선택된다.
노드 B에 대해 비용이 가장 작은 간선 a가 선택된다,
노드 C에 대해 비용이 가장 작은 간선 e가 선택된다.
노드 D에 대해 비용이 가장 작은 간선 g가 선택된다.
노드 E에 대해 비용이 가장 작은 간선 e가 선택된다.
노드 F에 대해 비용이 가장 작은 간선 c가 선택된다.
노드 G에 대해 비용이 가장 작은 간선 j가 선택된다.
노드 H에 대해 비용이 가장 작은 간선 p가 선택된다.
노드 I에 대해 비용이 가장 작은 간선 o가 선택된다.
노드 J에 대해 비용이 가장 작은 간선 m이 선택된다.
노드 K에 대해 비용이 가장 작은 간선 m이 선택된다.
이를 통해 선택된 간선들을 형광펜으로 표시하겠다,
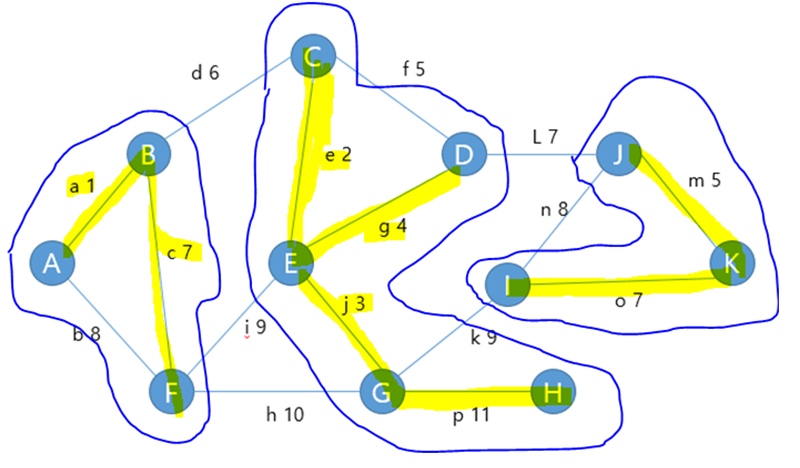
이렇게 각각의 덩어리진 트리들이 생기게 된다.
한 덩이가 된 트리에서 왼쪽의 트리를 기준으로 보았을 때 최소 비용의 간선은 간선 d, I, h중에서 d가 된다.
가운데 트리를 기준으로 최소 비용의 간선은 d가 된다.
오른쪽 트리를 기준으로 최소 비용의 간선은 l이 된다.
따라서 최종적은 트리 모양은 다음과 같다.
이때 각각의 비용의 합은 1+6+7+2+4+3+11+7+7+5 = 53 이다.
이렇게 대표적인 최소 신장 트리 알고리즘 3가지를 알아보았다.

제가 2019년 캠퍼스형 공동 교육과정에서 자료구조를 이수하며 정리한 것입니다.
최소 신장 트리 알고리즘
다정고등학교 이정민
- 크러스컬 알고리즘(Kruskal’s algorithm)
크러스컬 알고리즘은 변의 개수를 E 꼭짓점의 개수를 V라고 할 때 O(E log V) 의 시간 복잡도를 가진다.
크러스컬 알고리즘은 아래와 같이 작동한다.
1. 그래프의 각 꼭짓점이 각각 하나의 나무가 되도록 하는 숲A 를 만든다.
2. 모든 변을 원소로 하는 집합 S를 만든다.
3. 집합 S 가 비어있지 않는 동안
- 가장 작은 비용의 변을 S에서 하나 뺀다.
- 그 변이 어떤 두개의 나무를 연결한다면 두 나무를 연결하여 하나의 나무로 만든다.
- 그렇지 않다면 그 변은 버린다.
이와 다른 형태로, 변을 제거하는 방식이 존재한다.
1. 그래프에서 꼭짓점 또는 나무를 분리해 내지 않는 최대 가중치의 변을 제거한다.
2. 그래프에 n-1개 변만 남을 때까지 과정 1을 반복한다.
3. 그래프에 n-1개의 변이 남으면 최소 신장 트리이다.
예를 들어, 다음과 같은 그래프가 있다.

먼저 가장 비용이 낮은 a를 선택한다. 현재까지 비용은 1이다. 다음으로 계속해서 비용이 낮은 간선을 선택하되 고리가 만들어지지 않도록 한다.
이 점에 유의하여 선택하는 간선의 순서는 a – e – j – g – m (f는 순환이 만들어진다.) - d – c, l, o – p (n, b, k,i,h 는 순환이 만들어진다.) 순서이다.
따라서 비용은 1+2+3+4+5+6+7+7+7+11 = 53 이다.
- 프림 알고리즘 (Prim’s algorithm)
프림 알고리즘은 변의 개수를 E, 꼭짓점의 개수를 V 라고 하였을 때, 이진 힙을 사용하면 O(E log V)의 시간 복잡도를 가진다. 또한 그래프가 충분히 빽빽한 경우, 피보나치 힙을 사용하여 더 빠르게 할 수 있다, 이 방법은 복잡도가 O(E + V log V) 까지 떨어진다.
프림 알고리즘은 아래와 같은 순서로 작동한다.
1. 그래프에서 하나의 꼭짓점을 선택하여 트리를 만든다.
2. 그래프의 모든 변이 들어 있는 집합을 만든다.
3. 모든 꼭짓점이 트리에 포함되어 있지 않은 동안
- 트리와 연결된 변 가운데 트리 속의 두 꼭짓점을 연결하지 않는 가장 가중치가 작은 변을 트리에 추가한다.
알고리즘이 종료되었을 때, 만들어진 트리가 최소 신장 트리가 된다.
다음과 같은 그래프에서

임의의 노드를 잡는다. A를 잡겠다.
노드를 A로 잡을 경우 잡은 노드를 집합 T에 포함시킨다. 즉, T에는 노드 A가 들어있다. 이후 T에 있는 노드와 T에 없는 노드 사이에 간선 중 최소 비용인 간선을 찾는다. 찾은 간선이 연결하는 노드 중 T에 없는 노드를 T에 포함시키고 최소비용인 간선을 찾는 과정을 반복하면 된다.
A를 노드로 잡을 경우, 최소비용인 간선 a가 선택된다. 따라서 노드 B가 T에 포함되게 된다. 같은 원리로 찾다보면 다음과 같은 노드의 순서를 가진다.
A – B – C – E – G – D – F – J – K – I – H 따라서 최소비용은
1 + 6 + 2 + 3 +4 + 7 + 7+ 5 + 7+ 11 = 53이다.
- 솔린 알고리즘(Sollin’s algorithm)
솔린 알고리즘의 시간 복잡도는 변의 개수를 E 꼭짓점의 개수를 V라고 할 때 O(E log V)의 시간 복잡도를 가진다. 각 스텝마다 가능한 최선의 선택지를 고르는 것을 반복하여 결과를 얻어낸다.
솔린 알고리즘은 다음과 같이 작동한다.
1. 시작하면서 모든 정점을 트리로 정의한다. (포레스트 상태)
2. 하나의 트리에 대해 외부의 꼭짓점과 연결 가능한 가장 비용이 작은 간선을 선택해 추가한다.
- 간선이 중복되는 경우에는 하나만 선택한다.
3. 트리가 하나로 이어질 때까지 2를 반복한다.
알고리즘이 종료되었을 때, 최소 신장 트리가 된다.
다음과 같은 그래프에서

노드 A에 대해 비용이 가장 작은 간선 a가 선택된다.
노드 B에 대해 비용이 가장 작은 간선 a가 선택된다,
노드 C에 대해 비용이 가장 작은 간선 e가 선택된다.
노드 D에 대해 비용이 가장 작은 간선 g가 선택된다.
노드 E에 대해 비용이 가장 작은 간선 e가 선택된다.
노드 F에 대해 비용이 가장 작은 간선 c가 선택된다.
노드 G에 대해 비용이 가장 작은 간선 j가 선택된다.
노드 H에 대해 비용이 가장 작은 간선 p가 선택된다.
노드 I에 대해 비용이 가장 작은 간선 o가 선택된다.
노드 J에 대해 비용이 가장 작은 간선 m이 선택된다.
노드 K에 대해 비용이 가장 작은 간선 m이 선택된다.
이를 통해 선택된 간선들을 형광펜으로 표시하겠다,

이렇게 각각의 덩어리진 트리들이 생기게 된다.
한 덩이가 된 트리에서 왼쪽의 트리를 기준으로 보았을 때 최소 비용의 간선은 간선 d, I, h중에서 d가 된다.
가운데 트리를 기준으로 최소 비용의 간선은 d가 된다.
오른쪽 트리를 기준으로 최소 비용의 간선은 l이 된다.
따라서 최종적은 트리 모양은 다음과 같다.
이때 각각의 비용의 합은 1+6+7+2+4+3+11+7+7+5 = 53 이다.
이렇게 대표적인 최소 신장 트리 알고리즘 3가지를 알아보았다.
