머리말
안녕하세요 63um3um입니다.
이번 시간에는 제가 만든 남방진동지수 그래프와 예측 모델에 대해 글을 작성하려 합니다. (개인 프로젝트)
지구과학에 나온 개념인 엘니뇨, 라니냐, 남방진동, ENSO에 대해 배우고나서 남방진동 지수의 그래프를 python으로 표현하고자 하였고 이에 한 걸음 나아가서 처음으로 예측모델을 만들어보았습니다.
아이디어는 학교에 계신 지구과학 선생님이 주셨습니다. 3일동안 쉬지않고 만들었는데 거의 에러잡느라 고생을 했습니다..
코드는 여기있어용
nnT-Nje0n9/z9
Contribute to nnT-Nje0n9/z9 development by creating an account on GitHub.
github.com
개념
우선 그래프를 그린 남방진동에 대해 설명하겠습니다.
남방진동은 열대 태평양에서 호주 북부 다윈의 해면 기압과 남태평양 타히티의 해면기압의 차이를 분석한 것으로 시소처럼 서태평양의 기압이 높아지면 동태평양의 기압이 낮아지고, 동태평양의 기압이 높아지면 서태평양의 기압이 낮아집니다.
그럼 이것이 어떻게 엘니뇨, 라니냐와 관계가 있을까요? 평상시에 열대 태평양에서는 동에서 서쪽으로 부는 무역풍의 영향으로 해수의 흐름도 동쪽에서 서쪽(동태평양에서 서태평양)으로 나타나게 됩니다.
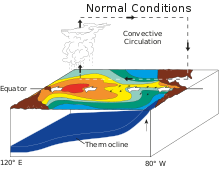
이런 식으로 흰색 화살표의 방향으로 해수가 흐르고 오른쪽에 해당하는 동태평양에서는 이동한 해수를 채우기 위해 용승이 일어나게 됩니다. 용승은 심층에서부터 찬 해수가 올라와서 동태평양의 온도가 낮아지게 됩니다.
반면 서태평양에서는 무역풍에 의해 서쪽으로 밀려나간 표면의 따뜻한 해수들이 모여서 온도가 상승하고 이로 인해 상승기류가 나타나게 됩니다. (저기압에선 상승기류가 나타나요)
따라서 서태평양은 동태평양보다 상대적으로 저기압인 상황이 만들어지고 당연하게도 서쪽에선 비가 많이 내리고 동쪽에선 아닌것이죠.
엘니뇨는 여기서 무역풍이 약화되는 것을 말하고 라니냐는 무역풍이 강화되는 것을 말합니다.
엘니뇨 시기에 무역풍이 약해져서 서쪽으로 흐르는 해수도 적어집니다.

그래서 끝까지 못가고 태평양 중앙부에 따뜻한 해수가 쌓이게 됩니다. 그러면 아까처럼 상승기류가 나타나고 저기압이 되는데 이 경우엔 태평양 중앙부가 되겠죠.
그림에서 보시다시피 용승의 양도 적어지고 동태평양은 그러면 평소보다 따뜻해져서 비가 내릴테고, 서태평양은 평소보다 고기압이라서 가뭄이 들겠습니다.
라니냐는 평소보다 무역풍이 강화되기에 다음과 같은 상황이 됩니다.
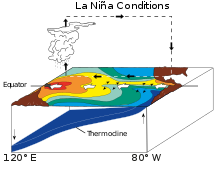
용승이 확 늘었다는 것을 알 수있고 서태평양에 따뜻한 해류가 더 치우쳐져 있습니다. 이는 평년에서 더 강화된 것으로 생각하면 되겠습니다. 서태평양은 엄청나게 저기압이 되어 홍수가 날 수도 있고, 반면에 동태평양은 더더더 고기압이라서 가뭄이 들겠네요.
여기서 서태평양은 다윈, 태평양 중앙부는 타히티, 동태평양은 페루입니다.
다윈 타히티 페루
평상시랑 엘니뇨는 반대
평상시랑 라니냐는 강화버전
그래서 정리하면
엘니뇨에선 다윈(서태평양)의 기압이 평년보다 높아지고 타히티(태평양 중앙)는 낮아집니다.
라니냐는 다윈의 기압이 평년보다 더 낮아지고 타히티는 높아집니다.
그래서 남방진동지수를 계산할 때 기압차를 이용한 SOI와 해수면 온도편차를 이용한 Nino 3.4가 있는데
SOI기준(수특에 나옴) (타히티 기압편차 - 다윈 기압편차)/표준편차이기 때문에
SOI지수가 양(+)의 값에서는 라니냐가 되고,
음(-)의 값은 엘니뇨가 됩니다.
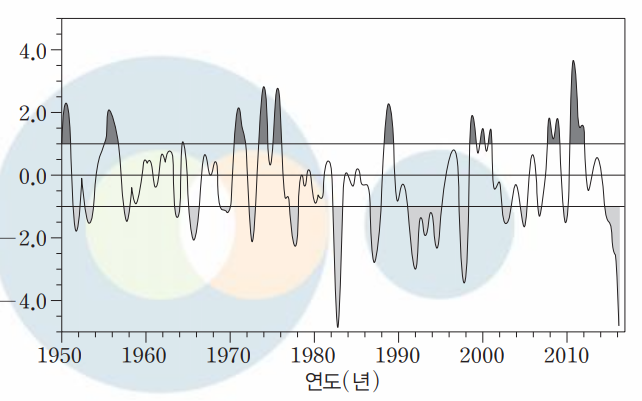
해당 그림에서 표준편차보다 높은 진한 부분이 라니냐가 심하게 일어났다고 볼수 있겠네요.
연한 부분은 엘니뇨.
PROGRAMMING
해당 코드에서는 4가지 모듈을 사용합니다.
numpy, pandas, matplotlib, statsmodels
numpy는 수학계산, pandas는 데이터를 처리하기 위함, matplotlib는 그래프그리기, statsmodels는 예측모델을 만들기 위함입니다.
해당 코드에 주석을 넣어두었으니 이해하기 쉬울 겁니다.
먼저 1950년대부터 2020년대까지 남방진동지수를 그래프에 그리기 위해서 데이트를 받아옵니다. 시계열 데이터에 대해 검색해보니 보통 csv파일을 가지고 많이 하기에
검색 키워드는 SOI csv로 했습니다.
NOAA(미국 해양대기청)에서 정리해둔 csv파일을 pandas로 받습니다.
csv파일을 받을때 시간을 처리할 때 에러가 자주 발생해서 일일이 데이터를 바꿔두고 깃허브에 올렸습니다.
matplotlib를 사용해서 그래프를 찍었습니다. 또한 표본집단의 표준편차를 계산했을 때 0.934867이 나왔고 이를 통해 다음과 같은 그래프를 얻었습니다.
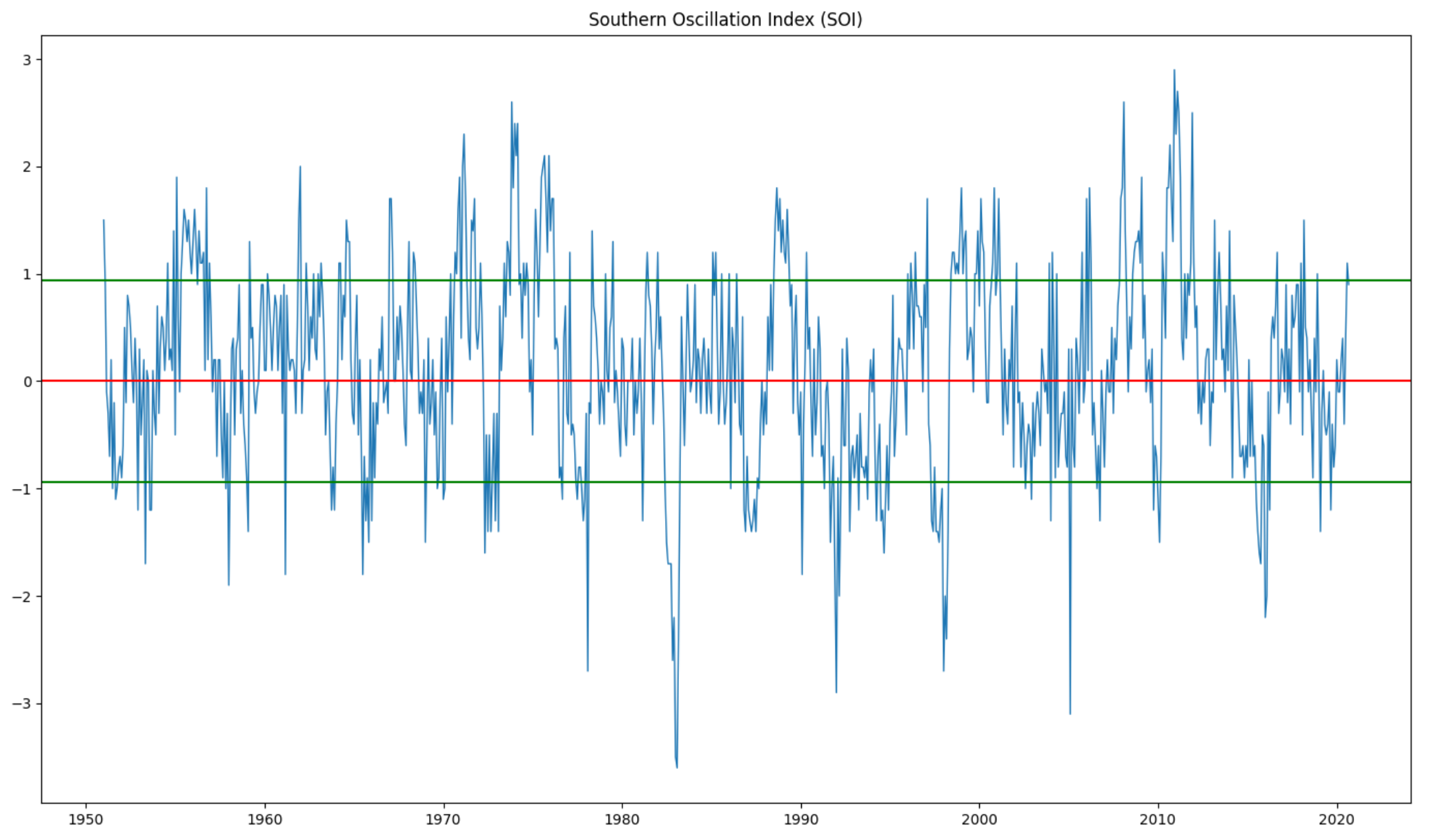
이후 시계열 데이터를 예측하기 위해서 자주 사용되는 ARIMA 모델을 가져다 쓰기로 했습니다.
ARIMA는 Autogressive Integrated Moving Average의 약자로 AR의 경우 자기회귀 모델, I는 차분, MA는 이동평균 모델을 의미합니다.
보통 ARIMA(AR,I,MA)식으로 사용합니다. 상황에 따라서 AR이 0이면 IMA, MA가 0이면 ARI, I가 0이면 ARMA모델이라고도 불립니다.
자기회귀모델 AR은 간단히 이전의 값이 이후의 값에 영향을 미치는 상황에 대해 이야기하며 정상성을 나타내는 데이터에 사용됩니다. 정상성을 나타내는 시계열은 추세나 계절성을 나타내는 시계열이 못된다고 해서 포기했습니다.
평균으로 돌아가려는 특징이 있는 데이터에 사용된다고 해서 자연은 그래도 관성이 있으니까 자기회귀모델을 사용해야하지 않을까? 생각하기도 했습니다.
이동평균모델 MR은 관측값이 이전의 연속적인 오차항의 영향을 받는다는 것입니다.
보통 ARIMA(p,d,q)에서 p+q<2, p*q=0인 모델을 많이 사용한다고 합니다.
그래서 AR인지 MA인지 판단하려면 ACF와 PACF그래프를 그려봐야 하기에 해당 코드도 삽입되어있습니다.
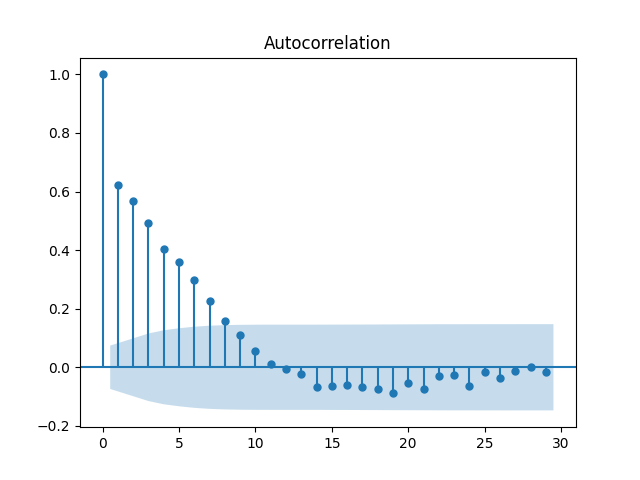
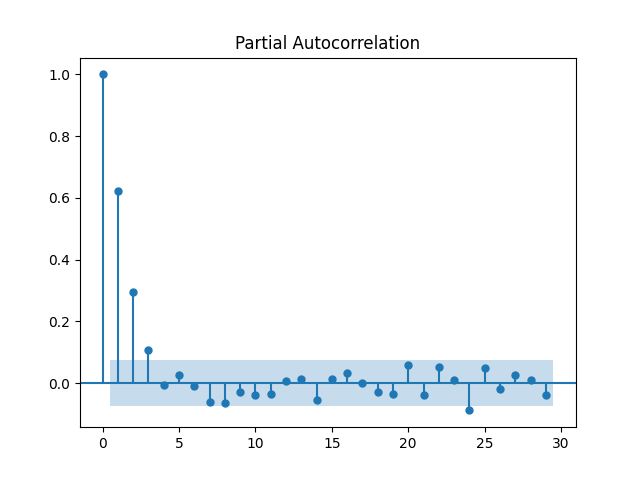
ACF : Time lag 기준 11에서 +에서 -로
PACF : 1회에 1.0 이후 급격히 감소입니다.
AR의 특성을 띄는 경우에 ACF는 천천히 감소하고 PACF는 처음 시차를 제외하고 급격히 감소한다고 하고
반대로, MA의 특성을 띄는 경우 ACF는 급격히 감소하고 PACF는 천천히 감소한다고 합니다. (정병기님의 글을 많이 참고했어요)
그래서 해당 그래프는 MA의 특성을 따릅니다.
차분을 몇번 해야하는지는 사실 잘 모르기에 여러개를 그려보면서 해봤어요.
결론적으로 ARIMA(0,2,1)을 따릅니다.
차분 2번해야 가장 잘 맞더라구요 소름돋았음
주석처리해뒀던 모델 summery는 다음을 따릅니다.
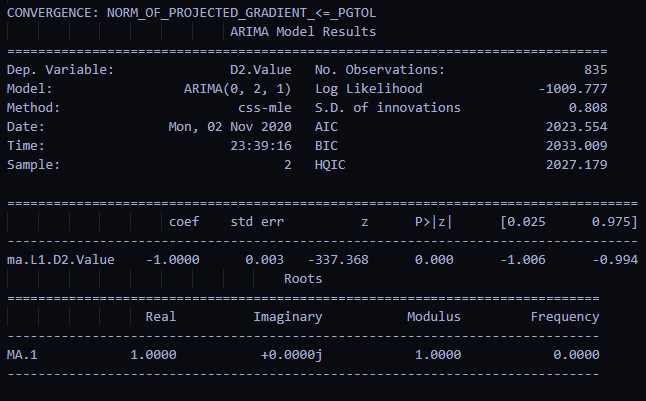
그래서 만든 프로그램을 실행시키면 아래 영상처럼 나오게 됩니다.
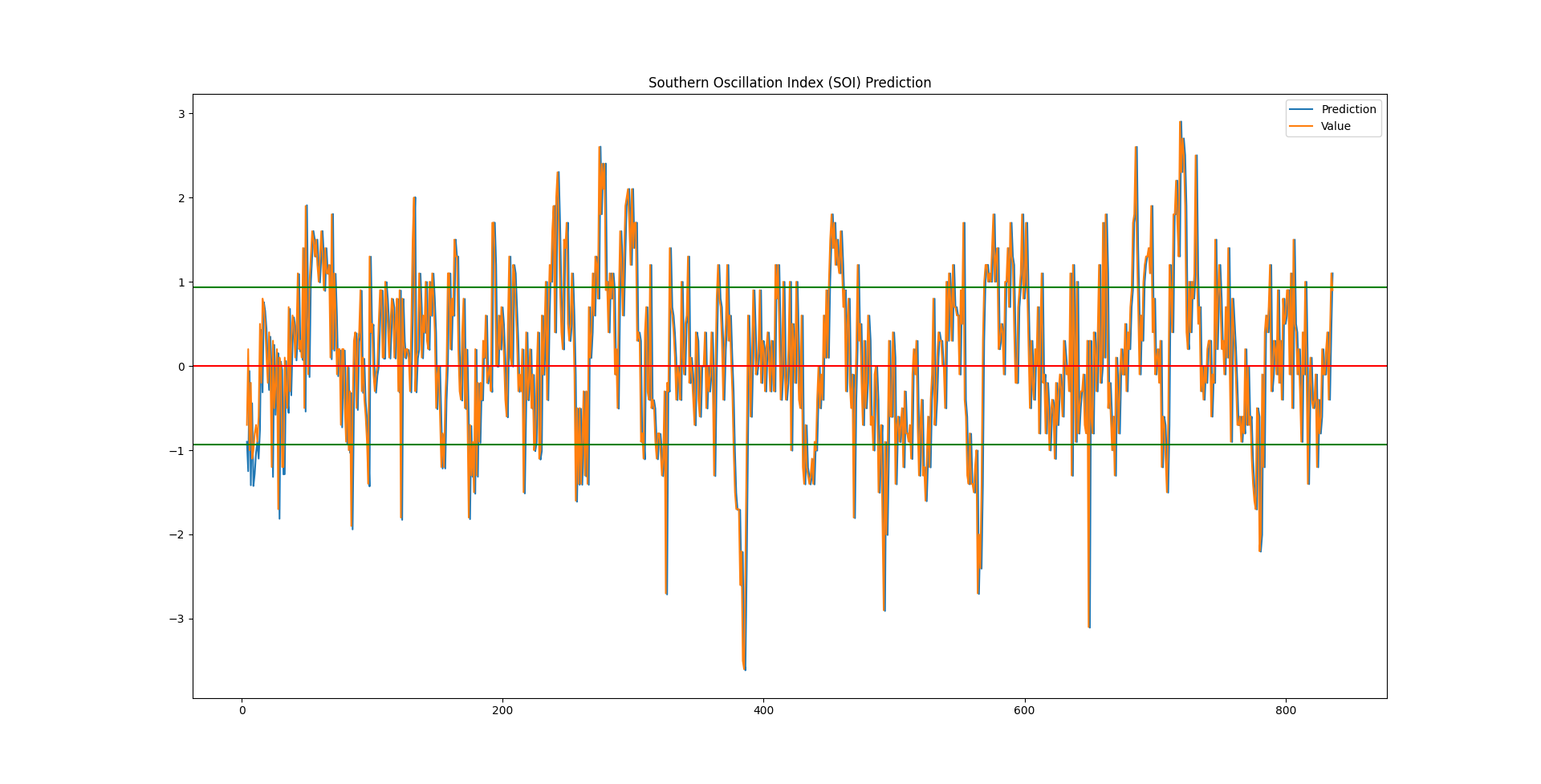
마치며
끝까지 읽어주셔서 감사합니다. 아직 전공도 아니고 부족한 것이 많음에도 불구하고 프로젝트중에 성공한것은 거의 처음이지 않았나 싶습니다.
서두에서 3일동안 쉬지않고 만들었다고 하는데 오늘까지 포함해서 4일이 되었네요. 이번 프로젝트로 느낀 점은 우선 제가 데이터 분석에 관심을 가지게 되었다는 것, 통계에서 예측모델에 관심을 가지게 된 것과 힘들더라도 포기하지 않고 며칠을 붙들며 했다는 점에서 뿌듯함을 느끼고 근성이 생겼다는 것입니다.
사실 3일,4일 이정도는 남들에겐, 그리고 현직 개발자분들에겐 얼마 안될수도 있겠지만, 나태한 저에게는 휴대폰 만질 시간에 에러에 대해 찾아보고 밥을 먹을 때에도 계속 이것만 들여다보았습니다.
저에게 이런 아이디어를 주신 지구과학 선생님께 큰 감사를 드리고 앞으로 더 발전된 모습을 보여드리겠습니다.
감사합니다.
머리말
안녕하세요 63um3um입니다.
이번 시간에는 제가 만든 남방진동지수 그래프와 예측 모델에 대해 글을 작성하려 합니다. (개인 프로젝트)
지구과학에 나온 개념인 엘니뇨, 라니냐, 남방진동, ENSO에 대해 배우고나서 남방진동 지수의 그래프를 python으로 표현하고자 하였고 이에 한 걸음 나아가서 처음으로 예측모델을 만들어보았습니다.
아이디어는 학교에 계신 지구과학 선생님이 주셨습니다. 3일동안 쉬지않고 만들었는데 거의 에러잡느라 고생을 했습니다..
코드는 여기있어용
nnT-Nje0n9/z9
Contribute to nnT-Nje0n9/z9 development by creating an account on GitHub.
github.com
개념
우선 그래프를 그린 남방진동에 대해 설명하겠습니다.
남방진동은 열대 태평양에서 호주 북부 다윈의 해면 기압과 남태평양 타히티의 해면기압의 차이를 분석한 것으로 시소처럼 서태평양의 기압이 높아지면 동태평양의 기압이 낮아지고, 동태평양의 기압이 높아지면 서태평양의 기압이 낮아집니다.
그럼 이것이 어떻게 엘니뇨, 라니냐와 관계가 있을까요? 평상시에 열대 태평양에서는 동에서 서쪽으로 부는 무역풍의 영향으로 해수의 흐름도 동쪽에서 서쪽(동태평양에서 서태평양)으로 나타나게 됩니다.

이런 식으로 흰색 화살표의 방향으로 해수가 흐르고 오른쪽에 해당하는 동태평양에서는 이동한 해수를 채우기 위해 용승이 일어나게 됩니다. 용승은 심층에서부터 찬 해수가 올라와서 동태평양의 온도가 낮아지게 됩니다.
반면 서태평양에서는 무역풍에 의해 서쪽으로 밀려나간 표면의 따뜻한 해수들이 모여서 온도가 상승하고 이로 인해 상승기류가 나타나게 됩니다. (저기압에선 상승기류가 나타나요)
따라서 서태평양은 동태평양보다 상대적으로 저기압인 상황이 만들어지고 당연하게도 서쪽에선 비가 많이 내리고 동쪽에선 아닌것이죠.
엘니뇨는 여기서 무역풍이 약화되는 것을 말하고 라니냐는 무역풍이 강화되는 것을 말합니다.
엘니뇨 시기에 무역풍이 약해져서 서쪽으로 흐르는 해수도 적어집니다.

그래서 끝까지 못가고 태평양 중앙부에 따뜻한 해수가 쌓이게 됩니다. 그러면 아까처럼 상승기류가 나타나고 저기압이 되는데 이 경우엔 태평양 중앙부가 되겠죠.
그림에서 보시다시피 용승의 양도 적어지고 동태평양은 그러면 평소보다 따뜻해져서 비가 내릴테고, 서태평양은 평소보다 고기압이라서 가뭄이 들겠습니다.
라니냐는 평소보다 무역풍이 강화되기에 다음과 같은 상황이 됩니다.

용승이 확 늘었다는 것을 알 수있고 서태평양에 따뜻한 해류가 더 치우쳐져 있습니다. 이는 평년에서 더 강화된 것으로 생각하면 되겠습니다. 서태평양은 엄청나게 저기압이 되어 홍수가 날 수도 있고, 반면에 동태평양은 더더더 고기압이라서 가뭄이 들겠네요.
여기서 서태평양은 다윈, 태평양 중앙부는 타히티, 동태평양은 페루입니다.
다윈 타히티 페루
평상시랑 엘니뇨는 반대
평상시랑 라니냐는 강화버전
그래서 정리하면
엘니뇨에선 다윈(서태평양)의 기압이 평년보다 높아지고 타히티(태평양 중앙)는 낮아집니다.
라니냐는 다윈의 기압이 평년보다 더 낮아지고 타히티는 높아집니다.
그래서 남방진동지수를 계산할 때 기압차를 이용한 SOI와 해수면 온도편차를 이용한 Nino 3.4가 있는데
SOI기준(수특에 나옴) (타히티 기압편차 - 다윈 기압편차)/표준편차이기 때문에
SOI지수가 양(+)의 값에서는 라니냐가 되고,
음(-)의 값은 엘니뇨가 됩니다.

해당 그림에서 표준편차보다 높은 진한 부분이 라니냐가 심하게 일어났다고 볼수 있겠네요.
연한 부분은 엘니뇨.
PROGRAMMING
해당 코드에서는 4가지 모듈을 사용합니다.
numpy, pandas, matplotlib, statsmodels
numpy는 수학계산, pandas는 데이터를 처리하기 위함, matplotlib는 그래프그리기, statsmodels는 예측모델을 만들기 위함입니다.
해당 코드에 주석을 넣어두었으니 이해하기 쉬울 겁니다.
먼저 1950년대부터 2020년대까지 남방진동지수를 그래프에 그리기 위해서 데이트를 받아옵니다. 시계열 데이터에 대해 검색해보니 보통 csv파일을 가지고 많이 하기에
검색 키워드는 SOI csv로 했습니다.
NOAA(미국 해양대기청)에서 정리해둔 csv파일을 pandas로 받습니다.
csv파일을 받을때 시간을 처리할 때 에러가 자주 발생해서 일일이 데이터를 바꿔두고 깃허브에 올렸습니다.
matplotlib를 사용해서 그래프를 찍었습니다. 또한 표본집단의 표준편차를 계산했을 때 0.934867이 나왔고 이를 통해 다음과 같은 그래프를 얻었습니다.

이후 시계열 데이터를 예측하기 위해서 자주 사용되는 ARIMA 모델을 가져다 쓰기로 했습니다.
ARIMA는 Autogressive Integrated Moving Average의 약자로 AR의 경우 자기회귀 모델, I는 차분, MA는 이동평균 모델을 의미합니다.
보통 ARIMA(AR,I,MA)식으로 사용합니다. 상황에 따라서 AR이 0이면 IMA, MA가 0이면 ARI, I가 0이면 ARMA모델이라고도 불립니다.
자기회귀모델 AR은 간단히 이전의 값이 이후의 값에 영향을 미치는 상황에 대해 이야기하며 정상성을 나타내는 데이터에 사용됩니다. 정상성을 나타내는 시계열은 추세나 계절성을 나타내는 시계열이 못된다고 해서 포기했습니다.
평균으로 돌아가려는 특징이 있는 데이터에 사용된다고 해서 자연은 그래도 관성이 있으니까 자기회귀모델을 사용해야하지 않을까? 생각하기도 했습니다.
이동평균모델 MR은 관측값이 이전의 연속적인 오차항의 영향을 받는다는 것입니다.
보통 ARIMA(p,d,q)에서 p+q<2, p*q=0인 모델을 많이 사용한다고 합니다.
그래서 AR인지 MA인지 판단하려면 ACF와 PACF그래프를 그려봐야 하기에 해당 코드도 삽입되어있습니다.


ACF : Time lag 기준 11에서 +에서 -로
PACF : 1회에 1.0 이후 급격히 감소입니다.
AR의 특성을 띄는 경우에 ACF는 천천히 감소하고 PACF는 처음 시차를 제외하고 급격히 감소한다고 하고
반대로, MA의 특성을 띄는 경우 ACF는 급격히 감소하고 PACF는 천천히 감소한다고 합니다. (정병기님의 글을 많이 참고했어요)
그래서 해당 그래프는 MA의 특성을 따릅니다.
차분을 몇번 해야하는지는 사실 잘 모르기에 여러개를 그려보면서 해봤어요.
결론적으로 ARIMA(0,2,1)을 따릅니다.
차분 2번해야 가장 잘 맞더라구요 소름돋았음
주석처리해뒀던 모델 summery는 다음을 따릅니다.

그래서 만든 프로그램을 실행시키면 아래 영상처럼 나오게 됩니다.

마치며
끝까지 읽어주셔서 감사합니다. 아직 전공도 아니고 부족한 것이 많음에도 불구하고 프로젝트중에 성공한것은 거의 처음이지 않았나 싶습니다.
서두에서 3일동안 쉬지않고 만들었다고 하는데 오늘까지 포함해서 4일이 되었네요. 이번 프로젝트로 느낀 점은 우선 제가 데이터 분석에 관심을 가지게 되었다는 것, 통계에서 예측모델에 관심을 가지게 된 것과 힘들더라도 포기하지 않고 며칠을 붙들며 했다는 점에서 뿌듯함을 느끼고 근성이 생겼다는 것입니다.
사실 3일,4일 이정도는 남들에겐, 그리고 현직 개발자분들에겐 얼마 안될수도 있겠지만, 나태한 저에게는 휴대폰 만질 시간에 에러에 대해 찾아보고 밥을 먹을 때에도 계속 이것만 들여다보았습니다.
저에게 이런 아이디어를 주신 지구과학 선생님께 큰 감사를 드리고 앞으로 더 발전된 모습을 보여드리겠습니다.
감사합니다.
