
내가 최근에 읽고 있는 책, 혹은 읽은 책 3가지가 연결된다.
1. 김대식의 인간 대 기계
2. 비트겐슈타인의 논리-철학 논고
3. 조너선 스타인히트 한권으로 읽는 컴퓨터 구조와 프로그래밍
1번은 추천받아서 읽었고, 2번은 철학적인 고민을 하다가 읽어보자 결심했다.
3번은 서점을 둘러보다 내가 공부하고 싶던 내용을 정확히 담고 있어서 읽었다.
3개 모두 좋은 책이다.
김대식의 인간 대 기계
읽은 순서는 논리-철학 논고가 먼저지만, 읽다가 포기했다.
'인간 대 기계'에서는 '논리-철학 논고'가 언급된다.
7가지 내용을 설명하면서 인간의 뇌에서 말로 표현되지 않는 부분을 설명하고자 했던 걸로 기억한다.
과거 서양 철학에 대한 이야기부터 비트겐슈타인에서 정리된 표현.
6. 진리 함수의 일반적 형식은 $[\overline{p},\overline{\xi},N(\overline{\xi})]$이다.
1. 세계는 일어나는 모든 것이다.
2. 일어나는 것, 즉 사실은 사태들의 존립이다.
3. 사실들의 논리적 그림이 사고이다.
4. 사고는 뜻이 있는 명제이다.
5. 명제는 요소 명제들의 진리 함수이다. (요소 명제는 자기 자신의 진리 함수이다.)
6. 진리 함수의 일반적 형식은 $[\overline{p},\overline{\xi},N(\overline{\xi})]$이다.
7. 말할 수 없는 것에 관해서는 침묵해야 한다.
이전에도 우주를 표현하는 것(모든 논리)에 대한 NAND의 언급이 있었으나, 비트겐슈타인은
$[\overline{p},\overline{\xi},N(\overline{\xi})]$, 즉 NAND를 표현했습니다.
근데.. $[\overline{p},\overline{\xi},N(\overline{\xi})]$라는 말이 난해합니다.
비트겐슈타인의 논리-철학 논고
해당 식의 해석에 대해서는 저도 무슨 말인지는 잘 모르겠는데.
일단 얘기해보죠.
$[\overline{p},\overline{\xi},N(\overline{\xi})]$
Bertrand Russell의 서론에서 위 식에 대하여
$\overline{p}$는 모든 원자적 명제들을 나타낸다.
$\overline{\xi}$는 명제들의 임의의 집합을 나타낸다.
$N(\overline{\xi})$는 $\overline{\xi}$를 이루는 모든 명제들의 부정을 나타낸다고 했습니다.
때문에 $[\overline{p},\overline{\xi},N(\overline{\xi})]$는 원자적 명제들 중에서 임의의 선택을 하여 그 모두를 부정한 다음 그 원래의 명제들 중 임의의 것과 함께 방금 얻어진 명제들의 집합에서 임의의 선택을 함으로써 얻을 수 있는 모든것을 의미한다고 합니다.
이렇게 보면 조금 NAND에 대해서 이해가 되기도 합니다.
이 상징은 원자 명제들의 주어졌을 때 다른 모든 명제들이 생산될 수 있도록 도와주는 과정을 기술하려고 의도됩니다.
그 과정은 다음에 의존합니다.
a. 모든 진리 함수는 동시적 부정으로부터, 즉 $\neg p . \neg q$로부터 얻어질 수 있다는 셰퍼의 증명 ( .은 and 연산 $\land$을 의미)
b. 연언과 선언으로부터 일반적 명제들을 도출해 내는 비트겐슈타인의 이론
c. 명제는 오직 진리 함수에 대한 논항으로서만 다른 명제 속에 나타날 수 있다는 주장
기호에 대해 잠깐 짚고 넘어가죠.
$\xi$ : 명제 변항을 의미
$\overline{\xi}$ : 명제 변항 $\xi$의 값이 되는 명제들 전부의 모음.
$N(\overline{\xi})$ : 명제 변항 $\xi$의 값 전부의 부정
$[a,x,O'x]$ : a, O'a, O'O'a, .... 라는 형식 계열의 일반항을 나타내는 표현
$[\overline{p},\overline{\xi},N(\overline{\xi})]$ : 진리 함수의 일반적 형식. 즉, 모든 명제는 각각 $N(\overline{\xi})$라는 연산을 요소 명제들에 계속 적용한 결과라는 것. $\overline{p}$는 요소 명제들의 집합.
최근 NAND에 대해 읽고 다시 논리-철학 논고를 펴보았는데,
6.41 세계의 뜻은 세계 밖에 놓여 있지 않으면 안 된다. 세계 속에서 모든 것은 있는 그대로 있으며, 모든 것은 일어나는 그대로 일어난다; 세계 속에는 가치가 존재하지 않는다 - 그리고 만일 가치가 존재한다면, 그것은 아무 가치도 가지지 않을 것이다.
가치를 가진 어떤 가치가 존재한다면, 그것은 모든 사건과 어떠어떠하게-있음 밖에 놓여 있지 않으면 안 된다. 왜냐하면 모든 사건과 어떠어떠하게-있음은 우연적이기 때문이다.
그것을 비-우연적으로 만드는 것은 세계 속에 놓여 있을 수 없다. 왜냐하면 그렇지 않다면 그것은 다시 우연적일 터이기 때문이다.
그것은 세계 밖에 놓여 있어야 한다.
6.5 언표될 수 없는 대답에 대해서는 물음도 언표될 수 없다.
수수께끼는 존재하지 않는다.
도대체 어떤 물음이 제기될 수 있다면, 그 물음은 또한 대답될 수도 있다.
6.51 회의주의는, 만일 그것이 물음이 있을 수 없는 곳에서 의심하고자 한다면, 반박 불가능한 것이 아니라 명백히 무의미한 것이다.
왜냐하면 의심이란 오직 물음이 존립하는 곳에서만 존립할 수 있고, 물음이란 대답이 존립할 수 있는 곳에서만 존립할 수 있으며, 또 이 대답이란 어떤 것이 말해질 수 있는 곳에서만 존립할 수 있기 때문이다.
6.52 비록 모든 가능한 과학적 물음들이 대답되어 있다 해도, 우리는 우리의 삶의 문제들이 여전히 조금도 건드려지지 않은 채로 있다고 느낀다. 물론 그렇다면 과연 아무런 물음도 더 이상 남아 있지 않다. 그리고 바로 이것이 대답이다.
6.521 삶의 문제의 해결은 이 문제의 소멸에서 발견된다.
7 말할 수 없는 것에 관해서는 침묵해야 한다.
이 책의 의미를 깨달으며 살아가는 의미를 고민하고 모든 것의 가치를 생각해보던 제게 큰 도움이 되었습니다.
https://gall.dcinside.com/mgallery/board/view/?id=reading&no=146130
논리철학논고 해석을 위한 도우미 3 - 비트겐슈타인이 말하는 삶의 의미 - 독서 갤러리
그림 형제의 우화 중 "어부와 그의 아내"라는 것이 있습니다.어부는 낚시를 하다가 넙치를 하나 잡았습니다. 그 넙치는 말을 할 수 있었고, 소원을 들어줄 테니 나를 풀어주라고 말했습니다.어부
gall.dcinside.com
한 권으로 읽는 컴퓨터 구조와 프로그래밍
NAND는 세상을 어떻게 표현할까요?
논리를 표현하는 기본적인 게이트는 AND, OR, NOT이 존재합니다.
이 세가지를 표현할 수 있다면 NAND는 우주를 표현할 수 있는게 아닐까요.
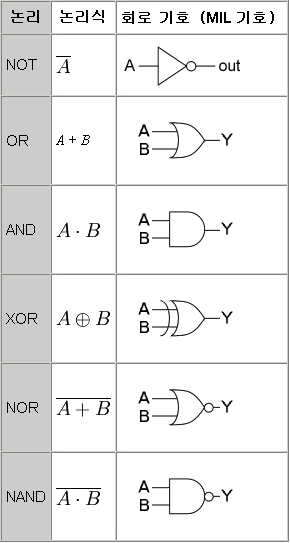
TTL(Transistor-Transistor Logic)이든 CMOS(Complementary Metal Oxide Semiconductor)든
논리 게이트에서 가장 단순한 회로는 NAND와 NOR이라고 합니다.
트랜지스터를 2개(TTL) 혹은 4개(CMOS)를 사용하는데, AND나 OR은 거기에 트랜지스터가 더 필요하고.. 그러면 느려지고.. 가격은 올라가고.. 하죠.
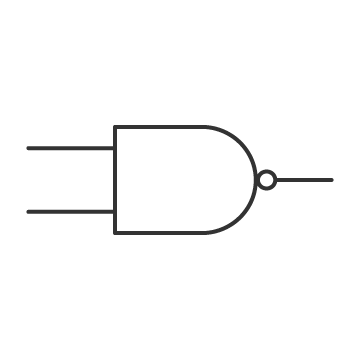
1. NOT 표현하기

A NAND A를 생각해보면
A가 1이면 not( 1 and 1) => 0
A가 0이면 not(0 and 0 ) => 1
NOT과 같이 작동합니다.
2. AND 표현하기
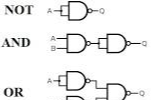
만들었던 not은 그대로 쓰고 NAND 뒤에 NOT을 붙이면 AND가 됩니다.
3. OR 표현하기
드모르간 법칙을 생각해봅시다.
\[\neg(A \lor B) = \neg A \land \neg B\]
\[\neg(A \land B) = \neg A \lor \neg B\]
논리합의 부정은 각각 부정의 논리곱
논리곱의 부정은 각각 부정의 논리합.
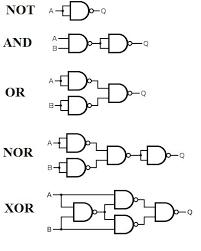
때문에 논리합 OR은 부정(NOT)의 논리곱의 부정(NAND)을 하면 되겠습니다.
$A \lor B = \neg(\neg A \land \neg B)$인데,
$\neg(A \land B)$가 NAND니까요.
오늘은 이렇게 연결된 세가지 책을 읽으며
느낀 점과 배운 점을 써봤습니다.
이과도 문과의 감성이, 문과도 이과의 감성이 필요한 것 같아요. 김상욱 교수님의 떨림과 울림, 양자 공부를 읽으면서도 느꼈지만
저는 자연과 논리로부터 인간 고민에 대한 깨달음 혹은 감성을 얻는 것을 매우 좋아합니다.
감사합니다.

내가 최근에 읽고 있는 책, 혹은 읽은 책 3가지가 연결된다.
1. 김대식의 인간 대 기계
2. 비트겐슈타인의 논리-철학 논고
3. 조너선 스타인히트 한권으로 읽는 컴퓨터 구조와 프로그래밍
1번은 추천받아서 읽었고, 2번은 철학적인 고민을 하다가 읽어보자 결심했다.
3번은 서점을 둘러보다 내가 공부하고 싶던 내용을 정확히 담고 있어서 읽었다.
3개 모두 좋은 책이다.
김대식의 인간 대 기계
읽은 순서는 논리-철학 논고가 먼저지만, 읽다가 포기했다.
'인간 대 기계'에서는 '논리-철학 논고'가 언급된다.
7가지 내용을 설명하면서 인간의 뇌에서 말로 표현되지 않는 부분을 설명하고자 했던 걸로 기억한다.
과거 서양 철학에 대한 이야기부터 비트겐슈타인에서 정리된 표현.
6. 진리 함수의 일반적 형식은 $[\overline{p},\overline{\xi},N(\overline{\xi})]$이다.
1. 세계는 일어나는 모든 것이다.
2. 일어나는 것, 즉 사실은 사태들의 존립이다.
3. 사실들의 논리적 그림이 사고이다.
4. 사고는 뜻이 있는 명제이다.
5. 명제는 요소 명제들의 진리 함수이다. (요소 명제는 자기 자신의 진리 함수이다.)
6. 진리 함수의 일반적 형식은 $[\overline{p},\overline{\xi},N(\overline{\xi})]$이다.
7. 말할 수 없는 것에 관해서는 침묵해야 한다.
이전에도 우주를 표현하는 것(모든 논리)에 대한 NAND의 언급이 있었으나, 비트겐슈타인은
$[\overline{p},\overline{\xi},N(\overline{\xi})]$, 즉 NAND를 표현했습니다.
근데.. $[\overline{p},\overline{\xi},N(\overline{\xi})]$라는 말이 난해합니다.
비트겐슈타인의 논리-철학 논고
해당 식의 해석에 대해서는 저도 무슨 말인지는 잘 모르겠는데.
일단 얘기해보죠.
$[\overline{p},\overline{\xi},N(\overline{\xi})]$
Bertrand Russell의 서론에서 위 식에 대하여
$\overline{p}$는 모든 원자적 명제들을 나타낸다.
$\overline{\xi}$는 명제들의 임의의 집합을 나타낸다.
$N(\overline{\xi})$는 $\overline{\xi}$를 이루는 모든 명제들의 부정을 나타낸다고 했습니다.
때문에 $[\overline{p},\overline{\xi},N(\overline{\xi})]$는 원자적 명제들 중에서 임의의 선택을 하여 그 모두를 부정한 다음 그 원래의 명제들 중 임의의 것과 함께 방금 얻어진 명제들의 집합에서 임의의 선택을 함으로써 얻을 수 있는 모든것을 의미한다고 합니다.
이렇게 보면 조금 NAND에 대해서 이해가 되기도 합니다.
이 상징은 원자 명제들의 주어졌을 때 다른 모든 명제들이 생산될 수 있도록 도와주는 과정을 기술하려고 의도됩니다.
그 과정은 다음에 의존합니다.
a. 모든 진리 함수는 동시적 부정으로부터, 즉 $\neg p . \neg q$로부터 얻어질 수 있다는 셰퍼의 증명 ( .은 and 연산 $\land$을 의미)
b. 연언과 선언으로부터 일반적 명제들을 도출해 내는 비트겐슈타인의 이론
c. 명제는 오직 진리 함수에 대한 논항으로서만 다른 명제 속에 나타날 수 있다는 주장
기호에 대해 잠깐 짚고 넘어가죠.
$\xi$ : 명제 변항을 의미
$\overline{\xi}$ : 명제 변항 $\xi$의 값이 되는 명제들 전부의 모음.
$N(\overline{\xi})$ : 명제 변항 $\xi$의 값 전부의 부정
$[a,x,O'x]$ : a, O'a, O'O'a, .... 라는 형식 계열의 일반항을 나타내는 표현
$[\overline{p},\overline{\xi},N(\overline{\xi})]$ : 진리 함수의 일반적 형식. 즉, 모든 명제는 각각 $N(\overline{\xi})$라는 연산을 요소 명제들에 계속 적용한 결과라는 것. $\overline{p}$는 요소 명제들의 집합.
최근 NAND에 대해 읽고 다시 논리-철학 논고를 펴보았는데,
6.41 세계의 뜻은 세계 밖에 놓여 있지 않으면 안 된다. 세계 속에서 모든 것은 있는 그대로 있으며, 모든 것은 일어나는 그대로 일어난다; 세계 속에는 가치가 존재하지 않는다 - 그리고 만일 가치가 존재한다면, 그것은 아무 가치도 가지지 않을 것이다.
가치를 가진 어떤 가치가 존재한다면, 그것은 모든 사건과 어떠어떠하게-있음 밖에 놓여 있지 않으면 안 된다. 왜냐하면 모든 사건과 어떠어떠하게-있음은 우연적이기 때문이다.
그것을 비-우연적으로 만드는 것은 세계 속에 놓여 있을 수 없다. 왜냐하면 그렇지 않다면 그것은 다시 우연적일 터이기 때문이다.
그것은 세계 밖에 놓여 있어야 한다.
6.5 언표될 수 없는 대답에 대해서는 물음도 언표될 수 없다.
수수께끼는 존재하지 않는다.
도대체 어떤 물음이 제기될 수 있다면, 그 물음은 또한 대답될 수도 있다.
6.51 회의주의는, 만일 그것이 물음이 있을 수 없는 곳에서 의심하고자 한다면, 반박 불가능한 것이 아니라 명백히 무의미한 것이다.
왜냐하면 의심이란 오직 물음이 존립하는 곳에서만 존립할 수 있고, 물음이란 대답이 존립할 수 있는 곳에서만 존립할 수 있으며, 또 이 대답이란 어떤 것이 말해질 수 있는 곳에서만 존립할 수 있기 때문이다.
6.52 비록 모든 가능한 과학적 물음들이 대답되어 있다 해도, 우리는 우리의 삶의 문제들이 여전히 조금도 건드려지지 않은 채로 있다고 느낀다. 물론 그렇다면 과연 아무런 물음도 더 이상 남아 있지 않다. 그리고 바로 이것이 대답이다.
6.521 삶의 문제의 해결은 이 문제의 소멸에서 발견된다.
7 말할 수 없는 것에 관해서는 침묵해야 한다.
이 책의 의미를 깨달으며 살아가는 의미를 고민하고 모든 것의 가치를 생각해보던 제게 큰 도움이 되었습니다.
https://gall.dcinside.com/mgallery/board/view/?id=reading&no=146130
논리철학논고 해석을 위한 도우미 3 - 비트겐슈타인이 말하는 삶의 의미 - 독서 갤러리
그림 형제의 우화 중 "어부와 그의 아내"라는 것이 있습니다.어부는 낚시를 하다가 넙치를 하나 잡았습니다. 그 넙치는 말을 할 수 있었고, 소원을 들어줄 테니 나를 풀어주라고 말했습니다.어부
gall.dcinside.com
한 권으로 읽는 컴퓨터 구조와 프로그래밍
NAND는 세상을 어떻게 표현할까요?
논리를 표현하는 기본적인 게이트는 AND, OR, NOT이 존재합니다.
이 세가지를 표현할 수 있다면 NAND는 우주를 표현할 수 있는게 아닐까요.

TTL(Transistor-Transistor Logic)이든 CMOS(Complementary Metal Oxide Semiconductor)든
논리 게이트에서 가장 단순한 회로는 NAND와 NOR이라고 합니다.
트랜지스터를 2개(TTL) 혹은 4개(CMOS)를 사용하는데, AND나 OR은 거기에 트랜지스터가 더 필요하고.. 그러면 느려지고.. 가격은 올라가고.. 하죠.

1. NOT 표현하기

A NAND A를 생각해보면
A가 1이면 not( 1 and 1) => 0
A가 0이면 not(0 and 0 ) => 1
NOT과 같이 작동합니다.
2. AND 표현하기
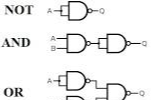
만들었던 not은 그대로 쓰고 NAND 뒤에 NOT을 붙이면 AND가 됩니다.
3. OR 표현하기
드모르간 법칙을 생각해봅시다.
\[\neg(A \lor B) = \neg A \land \neg B\]
\[\neg(A \land B) = \neg A \lor \neg B\]
논리합의 부정은 각각 부정의 논리곱
논리곱의 부정은 각각 부정의 논리합.

때문에 논리합 OR은 부정(NOT)의 논리곱의 부정(NAND)을 하면 되겠습니다.
$A \lor B = \neg(\neg A \land \neg B)$인데,
$\neg(A \land B)$가 NAND니까요.
오늘은 이렇게 연결된 세가지 책을 읽으며
느낀 점과 배운 점을 써봤습니다.
이과도 문과의 감성이, 문과도 이과의 감성이 필요한 것 같아요. 김상욱 교수님의 떨림과 울림, 양자 공부를 읽으면서도 느꼈지만
저는 자연과 논리로부터 인간 고민에 대한 깨달음 혹은 감성을 얻는 것을 매우 좋아합니다.
감사합니다.
