Modular Arithmetic의 시작
개념 설명
(Greatest Common Divisor을 최대공약수라고 한다.)
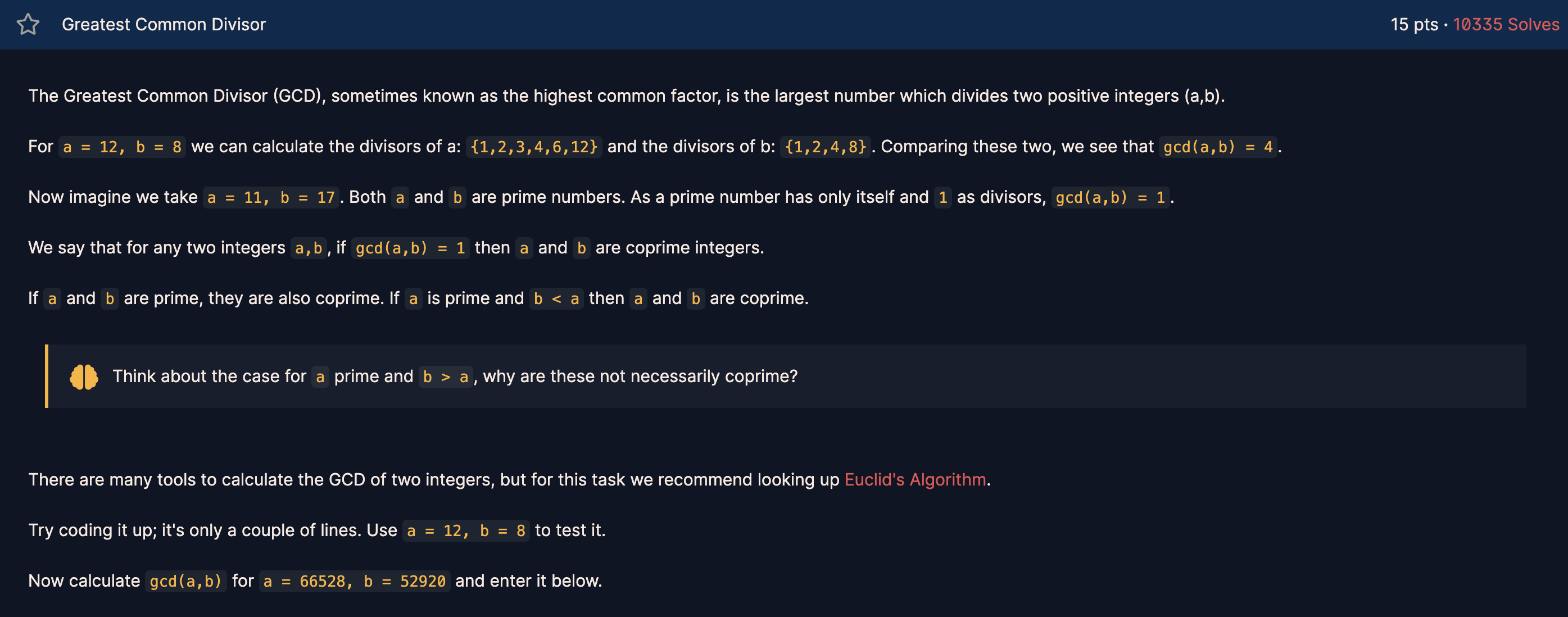
최대공약수(GCD)는 두개의 양의 정수 (a, b)를 나누는 가장 큰 약수로 알려져있다.
a=12, b=8의 경우 우리는 a: {1, 2, 3, 4, 6, 12}, b: {1, 2, 4, 8}로 약수를 계산할 수 있다. 이 둘을 비교하면 우리는 gcd(a, b) = 4라는 것을 알 수 있다.
이제 a=11, b=17을 예로 들어보자. a와 b는 모두 소수이다. 소수는 자기 자신과 1을 약수로 가지므로 gcd(a, b) = 1이다.
우리는 임의의 두 정수 a, b에 대해 gcd(a,b) = 1이면 a와 b는 서로소(coprime integers)라고 말한다.
a와 b가 소수라면(a != b여야 할듯?), 그들은 서로소이다. 만약 a가 소수이고 b < a이면 a와 b는 서로소이다.
! a가 소수이고 b > a일 경우를 생각해보자, 왜 이 둘은 반드시 서로소가 아닐까?
-> a를 11이라고 하고 b를 22라고 하자. 소수 p와 자연수 n을 곱해서 만드는 pn의 경우 p라는 최대공약수를 갖는다. 1이 아니다.
예제
두 정수의 GCD를 계산하는 도구는 많지만, 이 작업을 위해 우리는 유클리드 알고리즘(유클리드 호제법)에 대해 찾아볼 것을 권장한다.
그것을 코딩해보자. 몇 줄 밖에 안된다. a=12, b=8을 사용하여 테스트하라.
이제 a=66528, b=52920에 대한 gcd(a,b)를 계산하고 아래에 입력하자.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a%b)
print(gcd(66528, 52920))
재귀함수를 이용해서 코딩할 수 있다.
import math
print(math.gcd(66528, 52920))또는 math 모듈을 import 하여 math.gcd 함수를 사용할 수도 있다.
Modular Arithmetic의 시작
개념 설명

(Greatest Common Divisor을 최대공약수라고 한다.)
최대공약수(GCD)는 두개의 양의 정수 (a, b)를 나누는 가장 큰 약수로 알려져있다.
a=12, b=8의 경우 우리는 a: {1, 2, 3, 4, 6, 12}, b: {1, 2, 4, 8}로 약수를 계산할 수 있다. 이 둘을 비교하면 우리는 gcd(a, b) = 4라는 것을 알 수 있다.
이제 a=11, b=17을 예로 들어보자. a와 b는 모두 소수이다. 소수는 자기 자신과 1을 약수로 가지므로 gcd(a, b) = 1이다.
우리는 임의의 두 정수 a, b에 대해 gcd(a,b) = 1이면 a와 b는 서로소(coprime integers)라고 말한다.
a와 b가 소수라면(a != b여야 할듯?), 그들은 서로소이다. 만약 a가 소수이고 b < a이면 a와 b는 서로소이다.
! a가 소수이고 b > a일 경우를 생각해보자, 왜 이 둘은 반드시 서로소가 아닐까?
-> a를 11이라고 하고 b를 22라고 하자. 소수 p와 자연수 n을 곱해서 만드는 pn의 경우 p라는 최대공약수를 갖는다. 1이 아니다.
예제
두 정수의 GCD를 계산하는 도구는 많지만, 이 작업을 위해 우리는 유클리드 알고리즘(유클리드 호제법)에 대해 찾아볼 것을 권장한다.
그것을 코딩해보자. 몇 줄 밖에 안된다. a=12, b=8을 사용하여 테스트하라.
이제 a=66528, b=52920에 대한 gcd(a,b)를 계산하고 아래에 입력하자.
def gcd(a, b):
if b == 0:
return a
return gcd(b, a%b)
print(gcd(66528, 52920))
재귀함수를 이용해서 코딩할 수 있다.
import math
print(math.gcd(66528, 52920))또는 math 모듈을 import 하여 math.gcd 함수를 사용할 수도 있다.
