개념 설명
확장된 유클리드 알고리즘
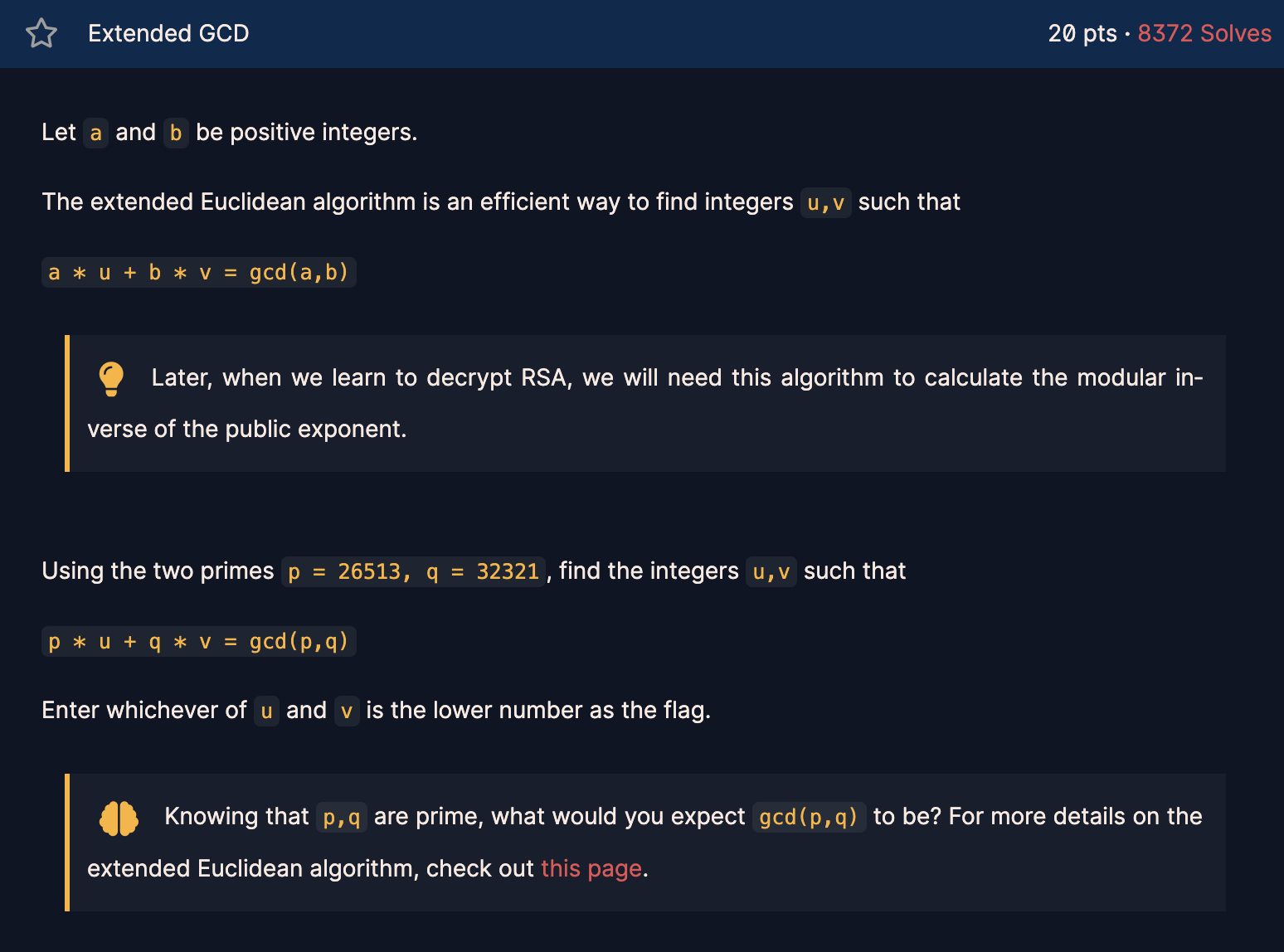
a와 b를 양의 정수로 하자.
확장된 유클리드 알고리즘은 다음과 같은 정수 u, v를 찾는 효율적인 방법이다.
a*u + b*v = gcd(a,b)
! 나중에 RSA를 해독하는 방법을 배울 때, Public exponent의 modular inverse를 계산하기 위해 이 알고리즘이 필요할 것이다.
두 소수 p = 26513, q = 33221을 사용하여 다음과 같은 정수 u, v를 구한다.
p*u + q*v = gcd(p, q)
u와 v중 낮은 숫자를 플래그로 입력한다.
! p와 q가 소수라는 것을 알고, gcd(p, q)가 무엇이라고 생각되는가? 확장된 유클리드 알고리즘에 대한 자세한 내용은 아래 페이지를 참조하자.
http://www-math.ucdenver.edu/~wcherowi/courses/m5410/exeucalg.html
Extended Euclidean Algorithm
The Extended Euclidean Algorithm As we know from grade school, when we divide one integer by another (nonzero) integer we get an integer quotient (the "answer") plus a remainder (generally a rational number). For instance, 13/5 = 2 ("the quotient") + 3/5 (
www-math.ucdenver.edu
라고는 하는데 해당 페이지로 접속이 안된다.
예제
def EEA(r1, r2, u1, u2, v1, v2) :
if r2 == 0:
print(f'gcd: {r1}\nu: {u1}\nv: {v1}')
return
q = r1//r2
r = r1%r2
u = u1 - q*u2
v = v1 - q*v2
return EEA(r2, r, u2, u, v2, v)
EEA(26513, 32321, 1, 0, 0, 1)
코드를 다음과 같이 작성했다.
확장된 유클리드 알고리즘의 원리를 인터넷에서 찾아봤는데
아래에서 따로 글을 작성했다.
개념 설명

확장된 유클리드 알고리즘
a와 b를 양의 정수로 하자.
확장된 유클리드 알고리즘은 다음과 같은 정수 u, v를 찾는 효율적인 방법이다.
a*u + b*v = gcd(a,b)
! 나중에 RSA를 해독하는 방법을 배울 때, Public exponent의 modular inverse를 계산하기 위해 이 알고리즘이 필요할 것이다.
두 소수 p = 26513, q = 33221을 사용하여 다음과 같은 정수 u, v를 구한다.
p*u + q*v = gcd(p, q)
u와 v중 낮은 숫자를 플래그로 입력한다.
! p와 q가 소수라는 것을 알고, gcd(p, q)가 무엇이라고 생각되는가? 확장된 유클리드 알고리즘에 대한 자세한 내용은 아래 페이지를 참조하자.
http://www-math.ucdenver.edu/~wcherowi/courses/m5410/exeucalg.html
Extended Euclidean Algorithm
The Extended Euclidean Algorithm As we know from grade school, when we divide one integer by another (nonzero) integer we get an integer quotient (the "answer") plus a remainder (generally a rational number). For instance, 13/5 = 2 ("the quotient") + 3/5 (
www-math.ucdenver.edu
라고는 하는데 해당 페이지로 접속이 안된다.
예제
def EEA(r1, r2, u1, u2, v1, v2) :
if r2 == 0:
print(f'gcd: {r1}\nu: {u1}\nv: {v1}')
return
q = r1//r2
r = r1%r2
u = u1 - q*u2
v = v1 - q*v2
return EEA(r2, r, u2, u, v2, v)
EEA(26513, 32321, 1, 0, 0, 1)
코드를 다음과 같이 작성했다.
확장된 유클리드 알고리즘의 원리를 인터넷에서 찾아봤는데
아래에서 따로 글을 작성했다.
