개념 설명
모듈러 연산
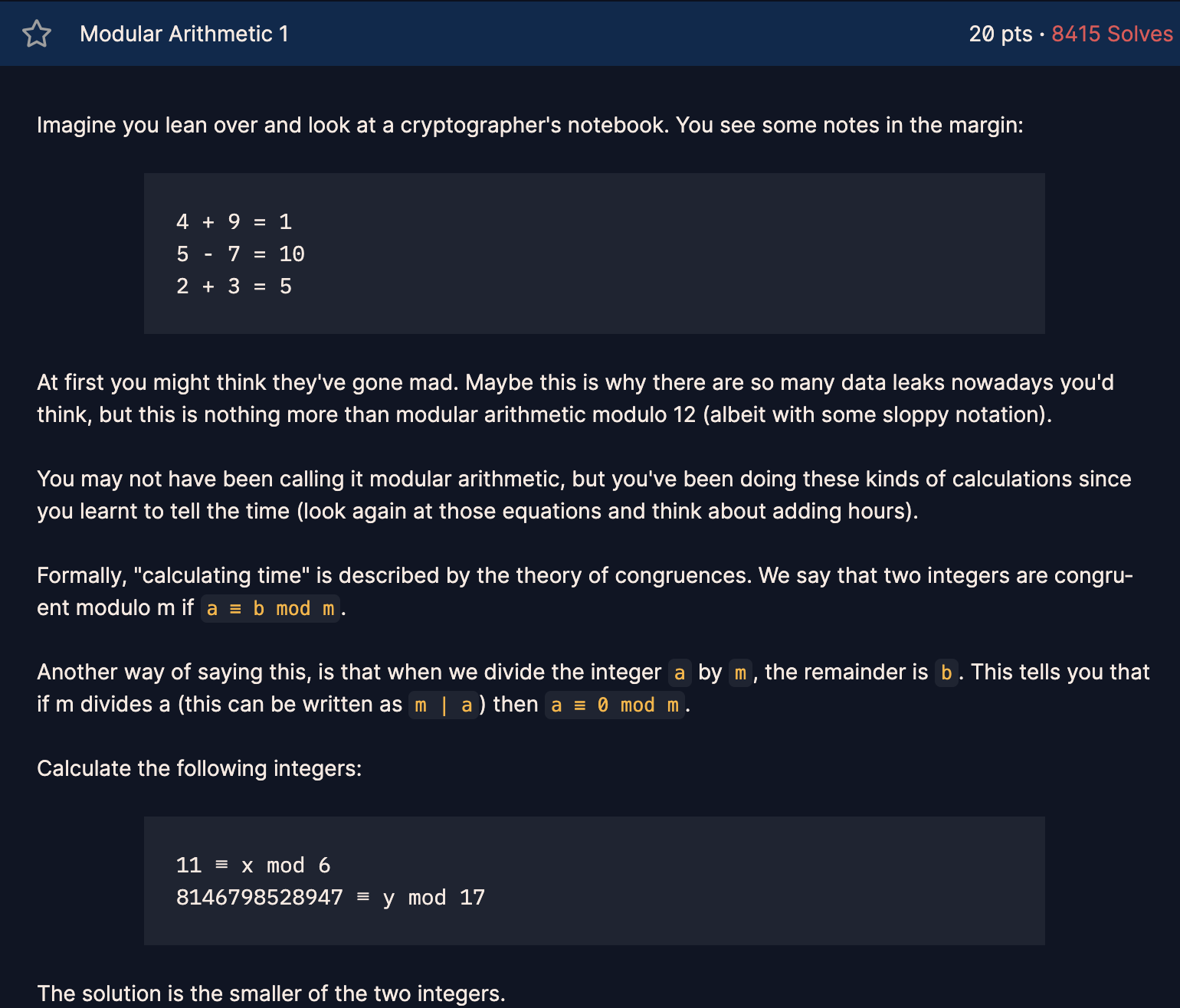
당신이 몸을 숙이고 암호학자의 노트를 본다고 상상해보라. 여백에 다음과 같은 참고 사항이 표기되어 있는 게 보인다.
4 + 9 = 1
5 - 7 = 10
2 + 3 = 5
처음엔 그들이 미쳤다고 생각할지도 모른다. 이것이 오늘날 많은 데이터유출의 이유라고 생각될 수도 있겠지만, 이것은 모듈러 12에 대한 모듈러 연산에 지나지 않는다. (비록 다소 엉성한 표기법일지라도 말이다.)
당신은 모듈러 연산을 사용해본 적이 없다고 할 수도 있겠지만, 당신은 시간을 말하는 법을 배운 이후로 이런 종류의 계산을 해오고 있다. (위 식을 다시 보고 시간을 더하는 것에 대해 생각해보라.)
형식적으로 "시간 계산"은 합동식 이론에 의해 설명된다. 우리는 두 정수가 $a \equiv b \bmod m$ 이면 a와 b가 법 m에 대해 합동이다 라고 말한다.
이것을 말하는 다른 방법은 우리가 정수 a를 m으로 나눌 때, 나머지가 b라는 것이다. 만약 m이 a를 나누면(나누어 떨어지면) (m | a라고 쓸 수 있다.) 이것을 $a \equiv 0 \bmod m$이라고 부른다.
나누어 떨어짐 기호(https://librewiki.net/wiki/%EB%82%98%EB%88%84%EC%96%B4%EB%96%A8%EC%96%B4%EC%A7%90)
나누어떨어짐
Divisibility
librewiki.net
예제
다음 정수를 계산하라.
11 ≡ x mod 6
8146798528947 ≡ y mod 17정답은 두 정수 중에서 작은 정수이다.
직접 계산하지 말고 컴퓨터한테 맡기자.
print(11 % 6)
print(8146798528947 % 17)python 코드로 작성해서 보면 2번째 줄 계산이 4로 더 작다.
개념 설명

모듈러 연산
당신이 몸을 숙이고 암호학자의 노트를 본다고 상상해보라. 여백에 다음과 같은 참고 사항이 표기되어 있는 게 보인다.
4 + 9 = 1
5 - 7 = 10
2 + 3 = 5
처음엔 그들이 미쳤다고 생각할지도 모른다. 이것이 오늘날 많은 데이터유출의 이유라고 생각될 수도 있겠지만, 이것은 모듈러 12에 대한 모듈러 연산에 지나지 않는다. (비록 다소 엉성한 표기법일지라도 말이다.)
당신은 모듈러 연산을 사용해본 적이 없다고 할 수도 있겠지만, 당신은 시간을 말하는 법을 배운 이후로 이런 종류의 계산을 해오고 있다. (위 식을 다시 보고 시간을 더하는 것에 대해 생각해보라.)
형식적으로 "시간 계산"은 합동식 이론에 의해 설명된다. 우리는 두 정수가 $a \equiv b \bmod m$ 이면 a와 b가 법 m에 대해 합동이다 라고 말한다.
이것을 말하는 다른 방법은 우리가 정수 a를 m으로 나눌 때, 나머지가 b라는 것이다. 만약 m이 a를 나누면(나누어 떨어지면) (m | a라고 쓸 수 있다.) 이것을 $a \equiv 0 \bmod m$이라고 부른다.
나누어 떨어짐 기호(https://librewiki.net/wiki/%EB%82%98%EB%88%84%EC%96%B4%EB%96%A8%EC%96%B4%EC%A7%90)
나누어떨어짐
Divisibility
librewiki.net
예제
다음 정수를 계산하라.
11 ≡ x mod 6
8146798528947 ≡ y mod 17정답은 두 정수 중에서 작은 정수이다.
직접 계산하지 말고 컴퓨터한테 맡기자.
print(11 % 6)
print(8146798528947 % 17)python 코드로 작성해서 보면 2번째 줄 계산이 4로 더 작다.
