http://www.kmooc.kr/courses/course-v1:DGUk+DGU_017k+DGU_007k_2021_9_17/course/
강좌 | DGU_017k | K-MOOC
www.kmooc.kr
1주차 학습 목표
1. 전기회로의 구성과 단위(Unit)를 이해할 수 있다.
2. 전기회로에 사용되는 전류, 전압, 전력 등의
주요 물리량을 이해할 수 있다.
3. 독립전원과 종속전원을 이해할 수 있다.
4. 종속전원의 네 가지 종류를 구분할 수 있다.
1주차에서는 회로를 해석하려는 기초를 공부하는 듯.
1. 전기 회로의 기초
회로(Eletric Circuit) : 전기 회로.
전기에서는 강전과 약전의 개념이 있는데, 전자는 약전에 속한다. 높아봤자 15V, 암페어는 마이크로 암페어 정도를 다루고 전기는 강전쪽에 속한다.
전기 회로에서는 물리량을 크게
전압, 전류, 전력을 들 수 있다.
회로는 Eletric Circuit 혹은 Eletric Network이런 개념이 있는데
회로와 회로망이라는 뜻이다. 회로망은 회로를 포함하는, 열려있는 큰 개념이다.
전기 소자는 Electric Circuit Element라고 한다.
R, L, C 등이 있으며, 트랜지스터는 보통 전자회로..이다.
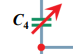
회로에서 화살표가 있으면 가변을 의미한다.
C : 커패시터(축전기)
L : 코일, 인덕터
R : 저항
소자에는 능동소자와 수동소자가 있다.
RLC와 같은 소자를 Passive Element라고 하고
트랜지스터 처럼 증폭같은 작용을 하는 것을 Active Element라고 한다.
물리량.
물리량의 단위에는 기본 단위와 유도 단위가 있다.
국제 단위계(SI)의 기본 단위이다.
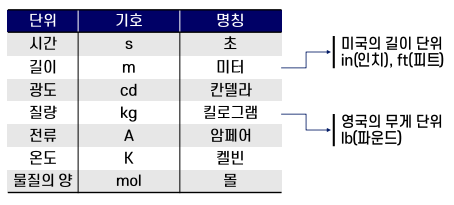
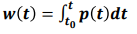
회로 이론에서 자주 볼 식인데,
P(t)는 전력이고 W(t)는 일이다.
물리량이 너무 크고 작을 경우를 하나의 Prefix를 가지고 간략하게 표현한다.
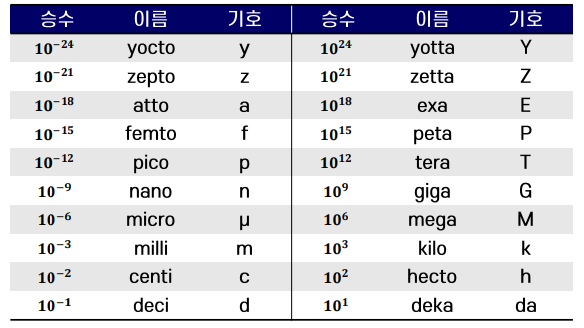
주로 milli, micro, nano
kilo, mega, giga.. 를 많이 쓰는데
10의 3의 배수 승이라고 외워두면 편하겠다.
기호에서 엄연히 대소문자는 구분해야한다.
Km 아니고 km
회로 해석.
선형 회로 해석은 두가지로 나뉜다.
직류 해석(DC analysis) 1~7장
과도 해석(transient analysis) 8~13장
DC : Direct Current
과도해석은 조금 변하는..
l과 c는 신호 자체가 한 번에 원하는 값이 쑥 나오지 않은데 이 때를 과도상태를 하고 이 상태를 다루는 것이 과도해석이다.
정현해석(sinusoidal Analysis) : 정상상태만 다룰텐데 sin, cos 함수같은 부분을 다룬다.
주파수 해석(frequency domain analysis) : 주파수 영역을 다룬다..
미분방정식으로 시간영역을 해석하는데 라플라스 해석과 푸리에 해석이 여기에 해당한다.
2. 전기 회로의 물리량
전기 회로의 물리량
전류 전압 전력
1. 전하(Eletric Charge)
전기적 현상을 설명하는 근본 개념이다.
원자에서 양성자, 중성자, 전자를 나타내듯이
기호는 시간에 따라 변하지 않는 경우 Q로 쓰고
시간에 따라 변하면 q를 쓴다.
단위는 [C] 쿨롱이다. (Coulomb)
전하는 새로이 만들어지거나 파괴될 수 없으며 단지 이동할 뿐이다. (전하 보존의 법칙)
전자의 전하량
-1.602 * 10^-19 C
양성자의 전하량
1.602 * 10^-19 C
1 C = 6.24 * 10^18 개의 전자
2. 전류
전하 흐름의 비율(The rate of charge flow)
기호는 I 또는 i로 쓴다.
단위는 암페어 [A]
1초 동안 1쿨롱의 전하 흐름이다.
따라서 1[A] = 1[C/s]
\[i(t) = {dq(t) \over dt}\]
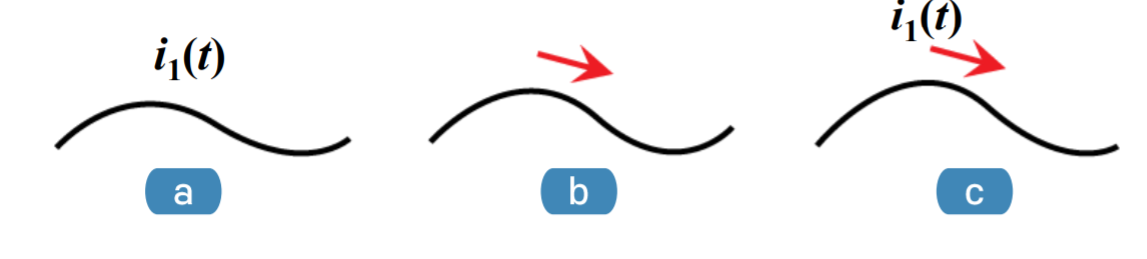
전류는 크기와 방향을 동시에 갖는다. 따라서 a처럼 크기만 표시하거나, b처럼 방향만 표시하는 것은 잘못되었다.
C와 같이 크기와 방향 모두 표시하는 것이 옳다.
벡터로 해석하면 될 듯
전류에는 직류와 교류가 있다.
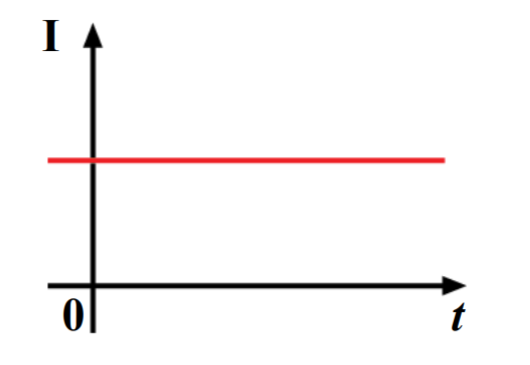
시간에 따라 전류가 변하지 않으면 직류이다. I
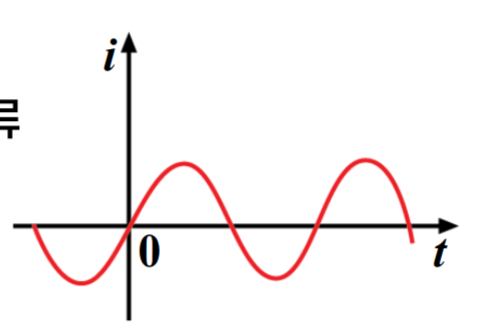
시간에 따라 변하면 교류이다. i
직류(Direct Current)
교류(Alternative Current)
3. 전압(Voltage)
두 위치에서 전기 포텐셜의 차이이다. 다른 말로는 전위차라고도 한다.
두 위치 사이에 단위 전하를 움직이기 위해 요구되는 에너지이다.
여기서 '단위 전하', '에너지'에 주목하자.
\[\therefore v = {dw \over dq}\]
라고 해석할 수도 있다.
\[[V] = [J/C]\]
기호는 V로 쓰고 단위도 [V] 이다. 볼트 라고 읽는다.

\[\pm\] 극성과 크기를 동시에 나타낸다. 3번째 회로처럼 표현하는 것이 옳다.
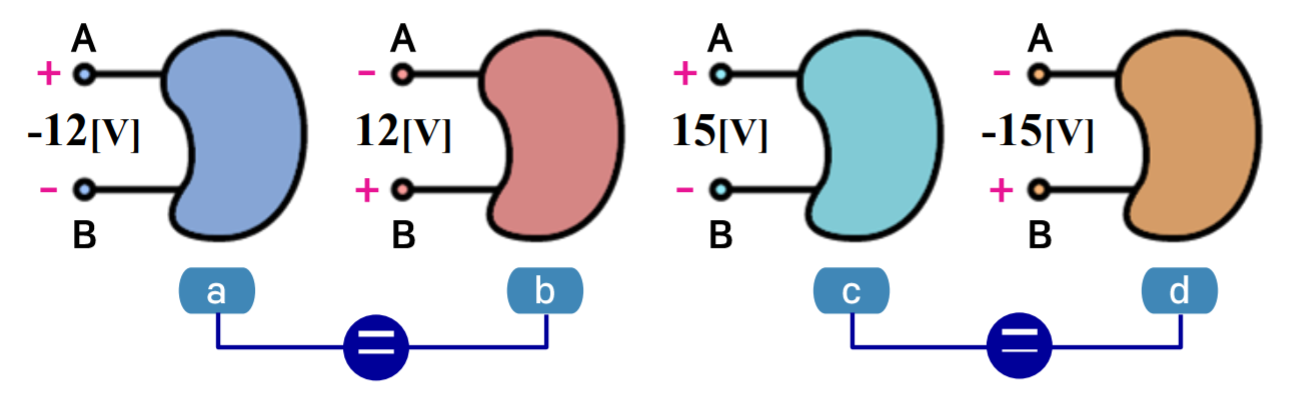
다음과 같이 옳게 나타낸 회로에서
극성이 바뀌면 전압의 부호도 바뀐다.
같다고 표시된 회로는 같은 것.
4. 전력(Power)
단위 시간당 전달되는 전기 에너지
\[\therefore P = {dw \over dt}\]
기호는 P를 쓰고 단위는 [W] 와트를 사용한다. 일의 기호 W와 헷갈리지 않도록 주의하자.
\[P = {dw \over dt} = {dW \over dq} \times {dq \over dt} = VI\]
\[\therefore P = VI\]
전력의 단위는 [W]이지만 내포된 의미는 [J/s]이다.
전력 말고도.
전기 요금을 계산하거나 할 때 전력'량'을 사용한다.
시간이 포함되어야 한다는 것이다.
전력에 시간을 곱해서
우리 주변에서 사용하는 전력량의 단위는 [kWh] 킬로와트시 이다.
P가 0보다 크면
에너지를 흡수한다.
RLC가 여기에 해당한다.
P가 0보다 작으면 에너지를 공급한다.
배터리가 여기에 해당한다.
수동 부호 규약(Passive Sign Convention)
"전압의 + 단자로 전류가 흘러들어가는 경우 양(+)의 전력을 소비한다고 정의한다"
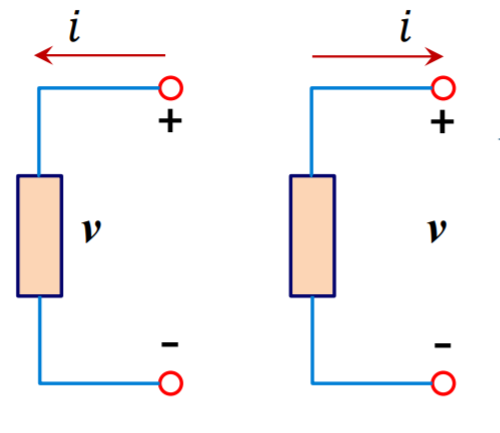
왼쪽 회로는 전력을 제공받는 소자(네모난 거)에서 +로부터 전류가 흘러 들어가니까 양(+)의 전력, 흡수한다.
오른쪽은 전력을 공급한다. 음(-)의 전력을 가진다. 배터리라고 생각해보면 이해된다.
6. 에너지 보존
\[W(t) = \int_{t_0}^{t} p(t)\ dt\]
단위는 [J]
1[Wh] = 1[W] * 3600[s] = 3600[J]
전력회사는 와트 * 시간으로 측정한다.
3. 전원의 이해
전기 회로를 구성하는 요소는 크게 2가지가 있다.
능동소자(Active Element)
: 에너지 공급
ex) 발전기, 배터리, 연산 증폭기 등
P<0
수동소자(Passive Element)
: 에너지 흡수
ex) 저항, 인덕터, 커패시터 (RLC)
P>0
이상적인 인덕터와 커패시터는 에너지를 소비하지 않지만 현실에서는 소모된다.
예를들면 휴대폰이 충전하고 가만히 있으면 방전되는..
전원의 구분.
전원에는 독립 전원(Independent Source)과 종속 전원(dependent Source)로 나뉜다.
전압원(Voltage Source)과 전류원(Current Source)으로도 나눌 수 있다.
1. (독립) 전압원
: 이상적인 전압 소스, 소자 양단에 걸쳐 지정된 전압을 유지하는 회로 요소이다.
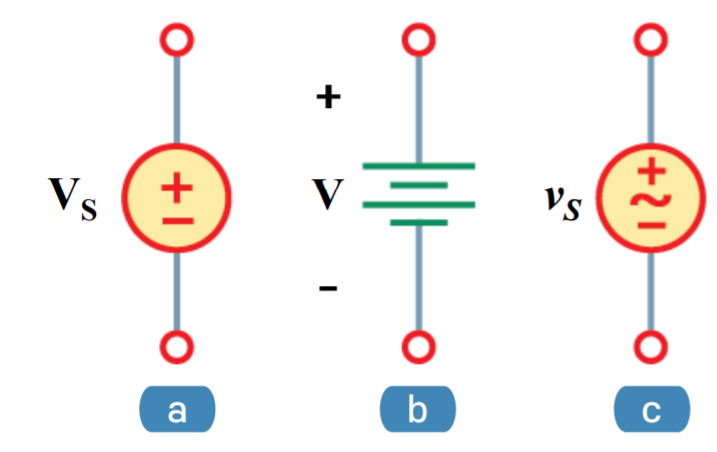
~표시가 없는 것을 직류 전압원 ~이 있는 것을 교류 전압원이라고 한다.
어떤 환경에서도 V_s를 공급한다.
b는 전지이다.
2. (독립)전류원
: 이상적인 전류 소스

직류 전류, 교류 전류
전류원에서 걸리는 전압은 회로를 해석해야 알 수 있고
전압원에서 걸리는 전류는 회로를 해석해야만 알 수 있다.
그러나 독립. 전압원과 전류원에서 전압과 전류는 각각 어느 환경에서도 일정하다.
동글동글하다 독립은.
종속 전원
: 종속 전원은 크게 4가지가 있다.
CCCS
VCCS
VCVS
CCVS
종속 전원은 다이아몬드로 생겼는데,
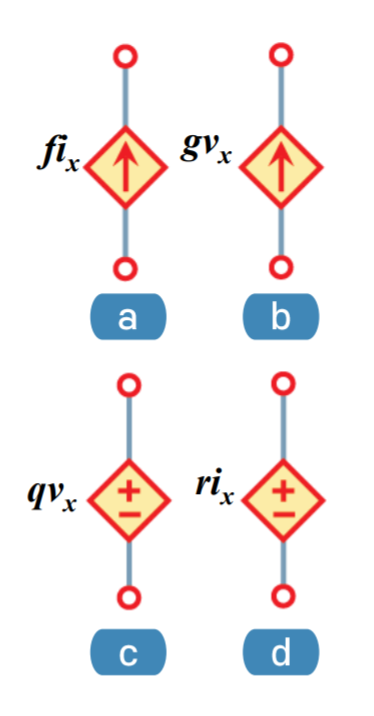
a와 b는 화살표가 나타나 있으므로 전류원
c와 d는 +-가 있으므로 전압원이다.
4개 모두 다이아몬드로 생겼으므로 종속이 붙는다.
a와 b는 종속 전류원
c, d는 종속 전압원
a에서 전류의 크기는
\[fi_x\]
b는
\[gv_x\]
이다.
c의 전압의 크기는 \[qv_x\]
d는 \[ri_x\]
이다.
\[f,g,q,r\]은 모두 상수이다.
\[i_x, v_x\]
전류나 전압을 결정하는 하나의 전류, 전압의 값을 의미한다.
a는 CCCS(Current Controlled Current Source)
: i_x에 의존하고 종속 전류원이므로
b는 VCCS(Voltage Controlled Current Source)
: v_x에 의존하고 종속 전류원이므로
c는 VCVS(Vlotage Controlled Voltage Source)
: v_x의존 종속 전압원
d는 CCVS(Current Controlled Voltage Source)
: i_x의존 종속 전압원
이렇게 4가지로 나뉜다.
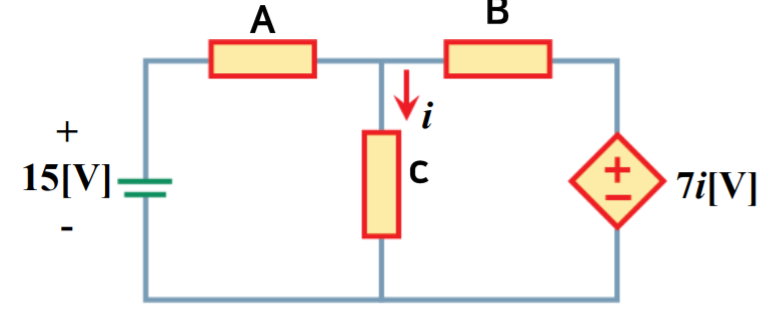
다음과 같은 예시에서
오른쪽 마름모는 전압원이고 전류i에 의해서 결정되므로
CCVS(Current Controlled Voltage Source)이다.
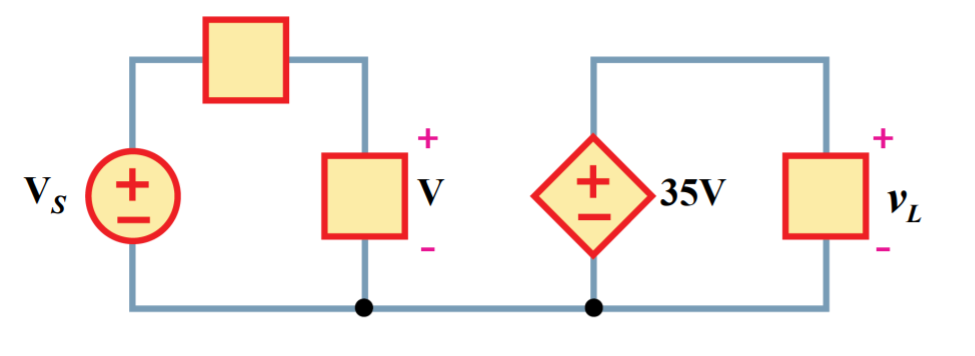
종속 전압원의 35V에서 V는 [V]단위가 아니다. V는 symbol이다.
VCVS(Voltage Controlled Voltage Source)이다.
왼쪽 사각형의 V에 의해 전압이 결정된다.
4. 문제 풀기

전류를 구하라고 했다.
전류는 단위 시간당 단위 전하량을 뜻한다.
\[i(t) = {dq(t) \over dt}\]
그래서 그냥 q(t)를 t에 대해 미분하면 된다.
\[q'(t) = 1200\pi \cos120\pi t = 1.2 \cos 120\pi t [kA]\]
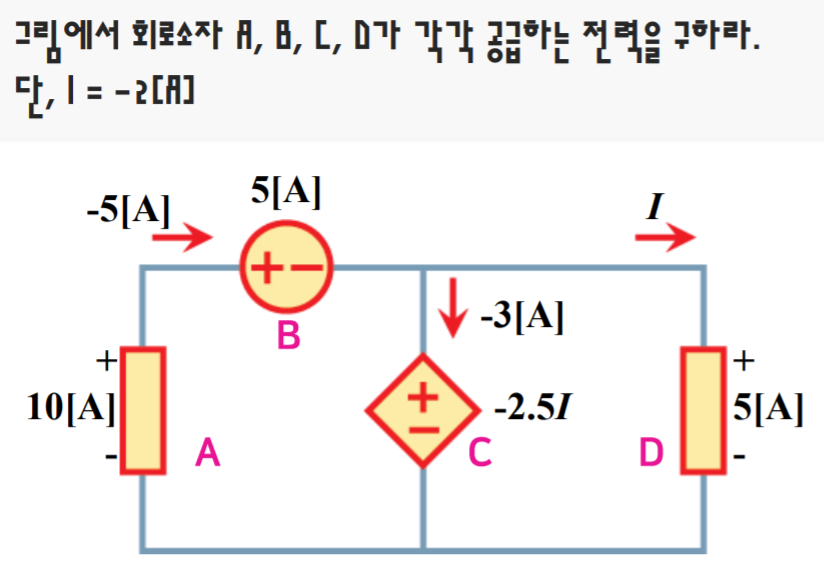
공급한다는 것은 P가 0보다 작다는 것을 의미한다.
PSC에서 +에서 전류가 흘러 나오는 것을 공급한다고 했으니
전력
\[p = vi\]
에서
? 교수님 A에서 10[V]로 고쳐야 할 거 같은데요..
문제를 이어서 풀면 A는 +- 로 적혀있으니 전압이 10[V]이고
전류는 +에서 흘러나오는 것 그대로 -5[A]이다.
\[\therefore P_A = -50[W]\]
이어서 B를 보자
B는 5[V]의 전압원이다.
PSC에 의해 +로 들어가는 전류가 생기므로 이는 흡수된다.
그래서 일단 -가 곱해져야하고(공급하는 것을 구하므로)
\[P_B = 5\times -5 \times -1 = 25[W]\]
를 공급한다.
C는 종속 전압원이다. CCVS이다.
I는.. -5와서 -3 빠지고 I 빠지니까 -2A이다.
그래서 C는 5[V]이다.
흘러 들어오고 있으니까 -를 붙여야한다.
\[\therefore P_C = -1\times -3\times 5 = 15[W]\]
같은 방법으로 D는
+로 들어오니까 - 붙여서
\[P_D = -1\times 5\times -2 = 10[W]\]
다 합쳐보면 -50 + 25 + 15 + 10 = 0
에너지는 보존된다.
1주차 끝!
http://www.kmooc.kr/courses/course-v1:DGUk+DGU_017k+DGU_007k_2021_9_17/course/
강좌 | DGU_017k | K-MOOC
www.kmooc.kr
1주차 학습 목표
1. 전기회로의 구성과 단위(Unit)를 이해할 수 있다.
2. 전기회로에 사용되는 전류, 전압, 전력 등의
주요 물리량을 이해할 수 있다.
3. 독립전원과 종속전원을 이해할 수 있다.
4. 종속전원의 네 가지 종류를 구분할 수 있다.
1주차에서는 회로를 해석하려는 기초를 공부하는 듯.
1. 전기 회로의 기초
회로(Eletric Circuit) : 전기 회로.
전기에서는 강전과 약전의 개념이 있는데, 전자는 약전에 속한다. 높아봤자 15V, 암페어는 마이크로 암페어 정도를 다루고 전기는 강전쪽에 속한다.
전기 회로에서는 물리량을 크게
전압, 전류, 전력을 들 수 있다.
회로는 Eletric Circuit 혹은 Eletric Network이런 개념이 있는데
회로와 회로망이라는 뜻이다. 회로망은 회로를 포함하는, 열려있는 큰 개념이다.
전기 소자는 Electric Circuit Element라고 한다.
R, L, C 등이 있으며, 트랜지스터는 보통 전자회로..이다.

회로에서 화살표가 있으면 가변을 의미한다.
C : 커패시터(축전기)
L : 코일, 인덕터
R : 저항
소자에는 능동소자와 수동소자가 있다.
RLC와 같은 소자를 Passive Element라고 하고
트랜지스터 처럼 증폭같은 작용을 하는 것을 Active Element라고 한다.
물리량.
물리량의 단위에는 기본 단위와 유도 단위가 있다.
국제 단위계(SI)의 기본 단위이다.

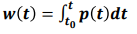
회로 이론에서 자주 볼 식인데,
P(t)는 전력이고 W(t)는 일이다.
물리량이 너무 크고 작을 경우를 하나의 Prefix를 가지고 간략하게 표현한다.

주로 milli, micro, nano
kilo, mega, giga.. 를 많이 쓰는데
10의 3의 배수 승이라고 외워두면 편하겠다.
기호에서 엄연히 대소문자는 구분해야한다.
Km 아니고 km
회로 해석.
선형 회로 해석은 두가지로 나뉜다.
직류 해석(DC analysis) 1~7장
과도 해석(transient analysis) 8~13장
DC : Direct Current
과도해석은 조금 변하는..
l과 c는 신호 자체가 한 번에 원하는 값이 쑥 나오지 않은데 이 때를 과도상태를 하고 이 상태를 다루는 것이 과도해석이다.
정현해석(sinusoidal Analysis) : 정상상태만 다룰텐데 sin, cos 함수같은 부분을 다룬다.
주파수 해석(frequency domain analysis) : 주파수 영역을 다룬다..
미분방정식으로 시간영역을 해석하는데 라플라스 해석과 푸리에 해석이 여기에 해당한다.
2. 전기 회로의 물리량
전기 회로의 물리량
전류 전압 전력
1. 전하(Eletric Charge)
전기적 현상을 설명하는 근본 개념이다.
원자에서 양성자, 중성자, 전자를 나타내듯이
기호는 시간에 따라 변하지 않는 경우 Q로 쓰고
시간에 따라 변하면 q를 쓴다.
단위는 [C] 쿨롱이다. (Coulomb)
전하는 새로이 만들어지거나 파괴될 수 없으며 단지 이동할 뿐이다. (전하 보존의 법칙)
전자의 전하량
-1.602 * 10^-19 C
양성자의 전하량
1.602 * 10^-19 C
1 C = 6.24 * 10^18 개의 전자
2. 전류
전하 흐름의 비율(The rate of charge flow)
기호는 I 또는 i로 쓴다.
단위는 암페어 [A]
1초 동안 1쿨롱의 전하 흐름이다.
따라서 1[A] = 1[C/s]

전류는 크기와 방향을 동시에 갖는다. 따라서 a처럼 크기만 표시하거나, b처럼 방향만 표시하는 것은 잘못되었다.
C와 같이 크기와 방향 모두 표시하는 것이 옳다.
벡터로 해석하면 될 듯
전류에는 직류와 교류가 있다.

시간에 따라 전류가 변하지 않으면 직류이다. I

시간에 따라 변하면 교류이다. i
직류(Direct Current)
교류(Alternative Current)
3. 전압(Voltage)
두 위치에서 전기 포텐셜의 차이이다. 다른 말로는 전위차라고도 한다.
두 위치 사이에 단위 전하를 움직이기 위해 요구되는 에너지이다.
여기서 '단위 전하', '에너지'에 주목하자.
라고 해석할 수도 있다.
기호는 V로 쓰고 단위도 [V] 이다. 볼트 라고 읽는다.


다음과 같이 옳게 나타낸 회로에서
극성이 바뀌면 전압의 부호도 바뀐다.
같다고 표시된 회로는 같은 것.
4. 전력(Power)
단위 시간당 전달되는 전기 에너지
기호는 P를 쓰고 단위는 [W] 와트를 사용한다. 일의 기호 W와 헷갈리지 않도록 주의하자.
전력의 단위는 [W]이지만 내포된 의미는 [J/s]이다.
전력 말고도.
전기 요금을 계산하거나 할 때 전력'량'을 사용한다.
시간이 포함되어야 한다는 것이다.
전력에 시간을 곱해서
우리 주변에서 사용하는 전력량의 단위는 [kWh] 킬로와트시 이다.
P가 0보다 크면
에너지를 흡수한다.
RLC가 여기에 해당한다.
P가 0보다 작으면 에너지를 공급한다.
배터리가 여기에 해당한다.
수동 부호 규약(Passive Sign Convention)
"전압의 + 단자로 전류가 흘러들어가는 경우 양(+)의 전력을 소비한다고 정의한다"

왼쪽 회로는 전력을 제공받는 소자(네모난 거)에서 +로부터 전류가 흘러 들어가니까 양(+)의 전력, 흡수한다.
오른쪽은 전력을 공급한다. 음(-)의 전력을 가진다. 배터리라고 생각해보면 이해된다.
6. 에너지 보존
단위는 [J]
1[Wh] = 1[W] * 3600[s] = 3600[J]
전력회사는 와트 * 시간으로 측정한다.
3. 전원의 이해
전기 회로를 구성하는 요소는 크게 2가지가 있다.
능동소자(Active Element)
: 에너지 공급
ex) 발전기, 배터리, 연산 증폭기 등
P<0
수동소자(Passive Element)
: 에너지 흡수
ex) 저항, 인덕터, 커패시터 (RLC)
P>0
이상적인 인덕터와 커패시터는 에너지를 소비하지 않지만 현실에서는 소모된다.
예를들면 휴대폰이 충전하고 가만히 있으면 방전되는..
전원의 구분.
전원에는 독립 전원(Independent Source)과 종속 전원(dependent Source)로 나뉜다.
전압원(Voltage Source)과 전류원(Current Source)으로도 나눌 수 있다.
1. (독립) 전압원
: 이상적인 전압 소스, 소자 양단에 걸쳐 지정된 전압을 유지하는 회로 요소이다.

~표시가 없는 것을 직류 전압원 ~이 있는 것을 교류 전압원이라고 한다.
어떤 환경에서도 V_s를 공급한다.
b는 전지이다.
2. (독립)전류원
: 이상적인 전류 소스

직류 전류, 교류 전류
전류원에서 걸리는 전압은 회로를 해석해야 알 수 있고
전압원에서 걸리는 전류는 회로를 해석해야만 알 수 있다.
그러나 독립. 전압원과 전류원에서 전압과 전류는 각각 어느 환경에서도 일정하다.
동글동글하다 독립은.
종속 전원
: 종속 전원은 크게 4가지가 있다.
CCCS
VCCS
VCVS
CCVS
종속 전원은 다이아몬드로 생겼는데,

a와 b는 화살표가 나타나 있으므로 전류원
c와 d는 +-가 있으므로 전압원이다.
4개 모두 다이아몬드로 생겼으므로 종속이 붙는다.
a와 b는 종속 전류원
c, d는 종속 전압원
a에서 전류의 크기는
b는
이다.
c의 전압의 크기는
d는
이다.
전류나 전압을 결정하는 하나의 전류, 전압의 값을 의미한다.
a는 CCCS(Current Controlled Current Source)
: i_x에 의존하고 종속 전류원이므로
b는 VCCS(Voltage Controlled Current Source)
: v_x에 의존하고 종속 전류원이므로
c는 VCVS(Vlotage Controlled Voltage Source)
: v_x의존 종속 전압원
d는 CCVS(Current Controlled Voltage Source)
: i_x의존 종속 전압원
이렇게 4가지로 나뉜다.

다음과 같은 예시에서
오른쪽 마름모는 전압원이고 전류i에 의해서 결정되므로
CCVS(Current Controlled Voltage Source)이다.

종속 전압원의 35V에서 V는 [V]단위가 아니다. V는 symbol이다.
VCVS(Voltage Controlled Voltage Source)이다.
왼쪽 사각형의 V에 의해 전압이 결정된다.
4. 문제 풀기

전류를 구하라고 했다.
전류는 단위 시간당 단위 전하량을 뜻한다.
그래서 그냥 q(t)를 t에 대해 미분하면 된다.

공급한다는 것은 P가 0보다 작다는 것을 의미한다.
PSC에서 +에서 전류가 흘러 나오는 것을 공급한다고 했으니
전력
에서
? 교수님 A에서 10[V]로 고쳐야 할 거 같은데요..
문제를 이어서 풀면 A는 +- 로 적혀있으니 전압이 10[V]이고
전류는 +에서 흘러나오는 것 그대로 -5[A]이다.
이어서 B를 보자
B는 5[V]의 전압원이다.
PSC에 의해 +로 들어가는 전류가 생기므로 이는 흡수된다.
그래서 일단 -가 곱해져야하고(공급하는 것을 구하므로)
를 공급한다.
C는 종속 전압원이다. CCVS이다.
I는.. -5와서 -3 빠지고 I 빠지니까 -2A이다.
그래서 C는 5[V]이다.
흘러 들어오고 있으니까 -를 붙여야한다.
같은 방법으로 D는
+로 들어오니까 - 붙여서
다 합쳐보면 -50 + 25 + 15 + 10 = 0
에너지는 보존된다.
1주차 끝!
